【论文阅读：激光SLAM】 LVIO-SAM: A Multi-sensor Fusion Odometry via Smoothing and Mapping

摘要

使用传感器进行状态估计对于移动机器人的映射和导航至关重要。由于不同的传感器在环境中具有不同的性能，因此如何将不同的传感器融合在一起将是一个问题。

在本文中，我们提出了一种多传感器融合法 LVIO-SAM 通过平滑和映射融合了激光雷达、立体相机和惯性测量单元（IMU）。

来自 IMU 的预积分运动估计消除了点云畸变，并为激光雷达里程计优化生成了初始值。得到的激光雷达里程计用于估计IMU的偏置，并作为视觉里程计的初始值。视觉里程计用作整个系统运动估计的中间因素。为了确保实时性能，我们分别边缘化了旧的激光雷达扫描和视觉3D点（即局部地图），以进行姿态优化。

简介

使移动机器人能够执行任务并与现实世界中的人互动一直是推动科学家和工程师前进的长期目标。要解决的基本任务之一是赋予机器人位置和环境感。同时定位和映射 （SLAM） 算法旨在解决此任务。

状态估计是SLAM算法的核心。随着相机的普及和视觉SLAM算法的发展，社区也与计算机视觉领域和束调整（BA）等方法建立了深厚的联系。

• 基于视觉的状态估计器由于照明、小视场（FoV）、运动模糊等因素的影响，在实践中不够鲁棒。
• 激光雷达硬件的最新进展促进了基于激光雷达的状态估计的研究。激光雷达传感器的宽FoV、密度、范围和精度使其适用于导航、定位和测绘任务。在大多数情况下，基于 LiDAR 的 SLAM 系统已经证明了其在准确性和鲁棒性方面的优势。但是，纯LiDAR方法在某些退化的情况下会失败，例如通过无特征的隧道或笔直的走廊。
• 基于视觉的系统高效轻量级。然而，观测范围是有限的，它们依赖于良好的数据关联才能表现良好。因此，它们在没有许多视觉功能的环境中会失败。
• IMU 产生高频测量，这对于短间隔以纠正偏差是合理的，但漂移很快。

在本文中，我们提出了一种通过平滑和映射的多传感器融合里程计 LVIO-SAM 来解决上述问题。我们使用原始 IMU 测量来消除畸变点云，并估计激光雷达扫描期间的传感器运动。除了点云去畸变外，预积分运动还可以用作激光雷达测程优化的初始值。得到的激光雷达测距法用于估计因子图中IMU的偏置，同时估计视觉测程法中三维点三角测量的初始值。为了确保实时性能，我们维护了关键帧姿势的滑动窗口，并边缘化了旧的激光雷达扫描和视觉3D点。

我们工作的主要贡献是：

• 利用激光雷达的测量结果，立体摄像头和惯性传感器以紧耦合的方式融合它们。
• 维护一个滑动窗口，该窗口使用激光雷达和视觉测程法进行更新，而不是像激光雷达扫描的边缘/平面特征和跟踪的视觉特征点这样的观察，以简化融合系统。

相关工作

我们回顾了与我们的工作密切相关的现有工作，包括视觉里程计（VO），激光雷达惯性里程计（LIO）和激光雷达-视觉惯性里程计（LVIO）方法。

视觉里程计（VO）可分为两类：基于特征法和直接法。基于特征的方法通常提取稀疏点特征并最小化特征点的重投影误差，而直接方法最小化光度误差，不需要特征点。在我们的工作中，我们将考虑限制在立体相机上。在最流行的公开VO管道中，S-PTAM，ORB-SLAM2和Vins-Fsuion，是基于特征的，而S-DSO是基于直接方法的。VINS-Fusion是一款基于优化的多传感器状态估计器，可为自主应用（无人机、汽车和AR/VR）实现精确的自定位。

现有的激光雷达惯性里程计（LIO）工作可分为松耦合和紧耦合两大类。松耦合方法分别处理两个传感器以推断其运动约束，而紧密耦合方法通过联合优化直接融合激光雷达和惯性测量。

• 基于激光雷达的测程法正变得越来越流行，这要归功于Zhang等人的初步工作，他们提出了LOAM算法。LOAM 执行点特征到边缘/平面扫描匹配，以查找激光雷达扫描之间的对应关系。IMU 测量用于对激光雷达扫描进行去畸变，并在扫描匹配之前给出运动。LeGO-LOAM 和 A-LOAM 是 LOAM 算法系列，一个针对地面车辆映射任务进行了优化，另一个是 LOAM 的实现，它使用特征和谷神星求解器来简化代码结构。由于优化步骤中不使用IMU测量，因此可以将这些算法归类为松散耦合方法。
• 与松耦合方法相比，紧密耦合方法表现出更高的鲁棒性和准确性，因此近年来引起了越来越多的研究兴趣。在LIO-Mapping中，作者提出了一个基于图的优化框架，该框架共同优化了预集成的IMU测量和从最近的点对平面表示得出的3D平面因子。LINS 是第一个通过迭代误差状态卡尔曼滤波器 （ESKF）求解六自由度 （15-DOF） 自我运动的紧密耦合 LIO。 与前一种算法相比，LIO-SAM 优化了因子图中关键帧姿势的滑动窗口，以实现更高的精度和鲁棒性。同样，LiLi-OM 专为基于滑动窗口优化的传统和固态激光雷达而设计。

为了避免退化并使系统更加健壮，LVIO方法在一些最近的工作中进行了探索在 LIMO 中，作者提出了一种基于光束调整的视觉里程计系统。他们通过将激光雷达测量值重新投影到图像空间中并将其与视觉特征相关联来校正深度以确保正确的比例。VIL-SLAM 将 VIO 与基于激光雷达的测程法相结合，作为一个单独的子系统，用于紧密结合不同的传感器模式，而不是联合优化。同样，LVI-SLAM 由两个子系统组成，视觉惯性系统（VIS）和激光雷达惯性系统（LIS）。当其中一个子系统检测到故障时，这两个子系统可以独立运行，或者在检测到足够多的特征时联合运行。多态约束卡尔曼滤波（MSCKF）框架被许多方法采用。LIC-fusion 框架将稀疏视觉特征、IMU测量和LiDAR平面和边缘特征与基于MSCKF框架的在线时空校准相结合。然而，在最近的后续工作LIC-Fusion 2.0 中，作者介绍了一种基于滑动窗口的平面特征跟踪方法，用于高效处理3D LiDAR点云。R2LIVE 是一款强大的实时紧密耦合多传感器融合框架。在误差状态迭代卡尔曼滤波的框架内估计状态，并通过因子图优化进一步提高整体精度。LVI-SAM 由两个子系统组成：视觉惯性系统（VIS）和激光雷达惯性系统（LIS）。我们的方法最接近它，但我们将三个传感器的数据集中在一个系统中，并且只使用所有三个因素构建因子图。我们的系统使用一次IMU数据，而两次。

所提出的 LVIO-SAM 方法通过平滑和映射融合了激光雷达、立体摄像头和IMU。视觉里程计用作整个因子图的因子约束之间。它维护关键帧姿势的滑动窗口，如 LIO-SAM。通过融合不同类型的传感器测量，我们实现了更高精度和鲁棒性的状态估计。

方法论

系统概述

我们的目标是以高精度和鲁棒性实时估计配备激光雷达、立体摄像头和 IMU 的机器人的方向、位置和线速度。我们将世界框架表示为 $\mathbf{W}$，将机器人的身体框架表示为 $\mathbf{B}$.为了方便起见，我们还假设IMU框架与机器人身体框架重合。机器人状态可以写成：

$$\mathbf{X}_i=\left[\mathbf{R}_i, \mathbf{p}_i, \mathbf{v}_i, \mathbf{b}_i^{{g}},, \mathbf{b}_i^{{a}}\right]^{\mathbf{T}},$$

其中 $\mathbf{R}_i \in S O(3)$ 是旋转矩阵， $\mathbf{p}_i \in \mathbb{R}^3$ 是位移向量，$\mathbf{v}_i$ 为速度，$\mathbf{b}_i$ 为 IMU 的偏置，a 是加速度计，b是陀螺仪。从 $\mathbf{B}$ 到 $\mathbf{W}$ 的坐标变换表示为 $\mathbf{T}=[\mathbf{R} \mid \mathbf{p}]$，$\mathbf{T} \in S E(3)$。

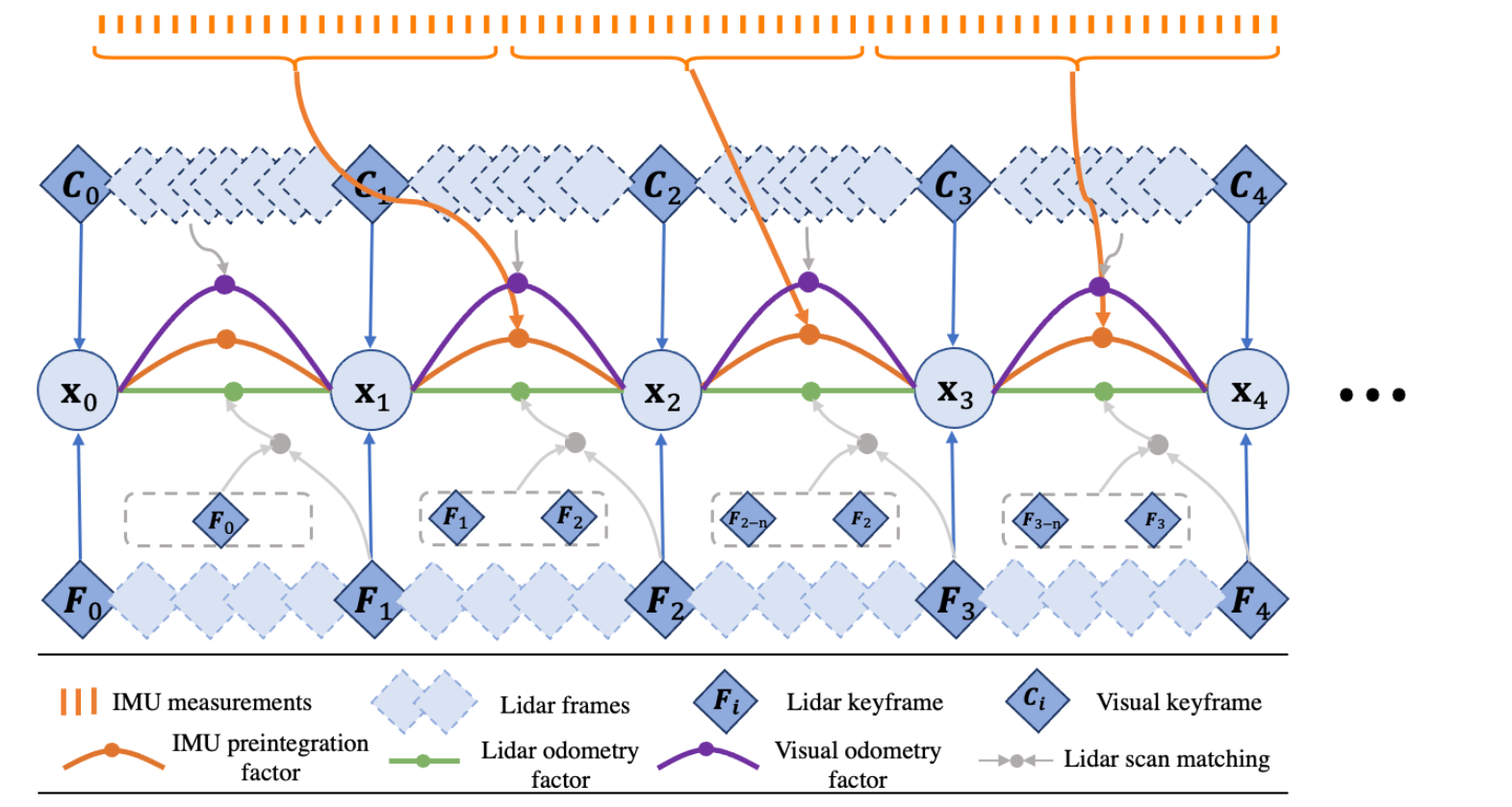
整个系统的结构如上图所示。该系统从3D激光雷达 ${\mathbf{F}}$ 、IMU ${\mathbf{I}}$ 和立体相机 ${\mathbf{C}}$ 接收不同时间和频率的传感器数据。时间的全套测量 $t_k$在滑动窗口中可以写成：

$$\mathbf{Z}_k=\left [ \left \{ F_i \right \} ,\left \{ I_j \right \} ,\left \{ C_l \right \} \right ]$$

我们的目标是估计机器人的状态 $\mathbf{X}_k$ 以及使用这些传感器的测量值的轨迹。这可以被认为是最大后验（MAP）问题：

$$\mathbf{X}_{k}=\operatorname{argmax} p\left(\mathbf{X}_{k} \mid \mathbf{Z}_{k}\right) \propto p\left(\mathbf{X}_{0}\right) p\left(\mathbf{Z}_{k} \mid \mathbf{X}_{k}\right)$$

等效于用高斯噪声模型的假设求解非线性最小二乘问题。我们构建了一个包含四种类型因子的因子图。具体而言，这四种类型的因子是 IMU 预积分因子、激光雷达里程计因子、视觉里程计因子和状态先验因子。因子图使用 GTSAM 的增量平滑和映射进行优化。以下各节介绍生成这些因素的过程。

IMU 预积分因子

** 与 LIO-SAM 推导相同

IMU 的角速度和加速度测量值由公式 2 和 3 确定：

$$\begin{aligned} & \hat{\omega}_t=\omega_t+\mathbf{b}_t^\omega+\mathbf{n}_t^\omega \\ & \hat{\mathbf{a}}_{\ell}=\mathbf{R}_t^{\mathrm{BW}}\left(\mathbf{a}_t-\mathbf{g}\right)+\mathbf{b}_t^{\mathbf{a}}+\mathbf{n}_t^{\mathbf{a}}, \end{aligned}$$

其中 $\hat{\boldsymbol{\omega}}_t$ 和 $\hat{\mathbf{a}}_t$ 是 IMU 在坐标系 $\mathbf{B}$ 下 $t$ 时刻的原始测量数据，而 $\hat{\boldsymbol{\omega}}_t$ 和 $\hat{\mathbf{a}}_t$ 同样都受到缓慢变化的偏置 $\mathbf{b}_t$ 和白噪声
$\mathbf{n}_t$ 的影响。$\mathbf{R}_t^{\mathbf{B W}}$ 是从坐标系 $\mathbf{W}$ 到 $\mathbf{B}$ 的转换变换矩阵。$\mathrm{g}$ 是坐标系 $\mathbf{W}$ 下的常数重力值。

现在可以使用 IMU 的测量值来推断机器人的运动。机器人在 $t+\Delta t$ 时刻的速度、位置和旋转可计算为:

$$\begin{aligned} \mathbf{v}_{t+\Delta t}=\mathbf{v}_t & +\mathbf{g} \Delta t+\mathbf{R}_t\left(\hat{\mathbf{a}}_t-\mathbf{b}_t^{\mathbf{a}}-\mathbf{n}_t^{\mathbf{a}}\right) \Delta t \\ \mathbf{p}_{t+\Delta t}=\mathbf{p}_t & +\mathbf{v}_t \Delta t+\frac{1}{2} \mathbf{g} \Delta t^2 \\ & +\frac{1}{2} \mathbf{R}_t\left(\hat{\mathbf{a}}_t-\mathbf{b}_t^{\mathbf{a}}-\mathbf{n}_t^{\mathbf{a}}\right) \Delta t^2 \\\mathbf{R}_{t+\Delta t}= & \mathbf{R}_t \exp \left(\left(\hat{\boldsymbol{\omega}}_t-\mathbf{b}_t^{\boldsymbol{\omega}}-\mathbf{n}_t^{\boldsymbol{\omega}}\right) \Delta t\right), \end{aligned}$$

其中 $\mathbf{R}_t=\mathbf{R}_t^{\mathbf{W B}}=\mathbf{R}_t^{\mathbf{B W} \mathbf{W}^{\top}}$。 这里我们假设在上述 $\Delta t$ 积分过程中，$\mathbf{B}$ 的角速度和加速度保持不变。

然后，我们使用 IMU 预积分方法来获得两个时间帧之间的物体相对运动。时间 $i$ 和 $j$ 之间的预积分测量 $\Delta \mathbf{v}_{i j}, \Delta \mathbf{p}_{i j}$ 和 $\Delta \mathbf{R}_{i j}$ 可以使用以下方法计算:

$$\begin{aligned}\Delta \mathbf{v}_{i j} & =\mathbf{R}_i^{\top}\left(\mathbf{v}_j-\mathbf{v}_i-\mathbf{g} \Delta t_{i j}\right) \\\Delta \mathbf{p}_{i j} & =\mathbf{R}_i^{\top}\left(\mathbf{p}_j-\mathbf{p}_i-\mathbf{v}_i \Delta t_{i j}-\frac{1}{2} \mathbf{g} \Delta t_{i j}^2\right) \\\Delta \mathbf{R}_{i j} & =\mathbf{R}_i^{\top} \mathbf{R}_j .\end{aligned}$$

除了效率之外，应用 IMU 预积分还自然而然地为我们提供了一种因子图约束–IMU 预积分因子。在因子图中，IMU 偏置与激光雷达里程因子共同优化。

激光雷达里程计因子

** 与 LIO-SAM 推导相同

当新的激光雷达扫描帧到达时，首先进行特征提取。通过评估局部区域内各点的粗糙度来提取边缘和平面特征。粗糙度值较大的点被归类为边缘特征。同样，粗糙度值较小的点被归类为平面特征。

我们将第 $i$ 时间激光雷达扫描提取的边缘和平面特征分别称为 $\mathrm{F} _{i}^{e}$ 和 $\mathrm{F} _{i}^{p}$。第 $i$ 个时间点提取的所有特征组成一个激光雷达帧 $\mathbb{F} _{i}$ ，其中 $\mathbb{F} _{i} = \{\mathrm{F} _{i}^{e} , \mathrm{F} _{i}^{p}\}$。请注意，激光雷达帧 $\mathbb{F}$ 是用 $\mathbf{B}$ 表示的。关于特征提取过程的更详细说明，请参阅 LOAM 文献，如果使用的是测距图像，则请参阅 LeGO-LOAM 文献。

$$\begin{gathered}\mathbf{d}_{e_k}=\frac{\left|\left(\mathbf{p}_{i+1, k}^e-\mathbf{p}_{i, u}^e\right) \times\left(\mathbf{p}_{i+1, k}^e-\mathbf{p}_{i, v}^e\right)\right|}{\left|\mathbf{p}_{i, u}^e-\mathbf{p}_{i, v}^e\right|} \\ \mathbf{d}_{p_k}=\frac{\left|\begin{array}{c}\left(\mathbf{p}_{i+1, k}^p-\mathbf{p}_{i, u}^p\right) \\ \left(\mathbf{p}_{i, u}^p-\mathbf{p}_{i, v}^p\right) \times\left(\mathbf{p}_{i, u}^p-\mathbf{p}_{i, w}^p\right) \end{array}\right|}{\left|\left(\mathbf{p}_{i, u}^p-\mathbf{p}_{i, v}^p\right) \times\left(\mathbf{p}_{i, u}^p-\mathbf{p}_{i, w}^p\right)\right|},\end{gathered}$$

其中 $k, u, v$, 和 $w$ 是相应集合中的特征索引。 对于${ }^{\prime} \mathrm{F}_{i+1}^e$ 中的边缘特征 $\mathbf{p}_{i+1, k}^e$ , $\mathbf{p}_{i, u}^e$ 和 $\mathbf{p}_{i, v}^e$是 $\mathbf{M}^e_i$ 中构成相应边缘线的点。 对于${ }^{\prime} \mathrm{F}_{i+1}^p$ 中的平面特征 $\mathbf{p}_{i+1, k}^p$ , $\mathbf{p}_{i, u}^p, \mathbf{p}_{i, v}^p$, 和 $\mathbf{p}_{i, w}^p$ 在 $\mathbf{M}^p_i$ 中构成相应的平面块。然后使用高斯牛顿法求解最优变换。

视觉里程计因子

当一对立体图像到达时，我们首先执行特征提取。在左图中提取角状特征 $C^l_k$ 并使用右图上的光流方法进行跟踪 $C^T_k$.同样，我们在两个连续的图像帧之间使用相同的方法跟踪特征。为了平衡计算资源和精度，我们使用滑动窗口求解机器人的3D点和相机姿势。下图显示了特征跟踪过程以及时空图像帧之间的约束。

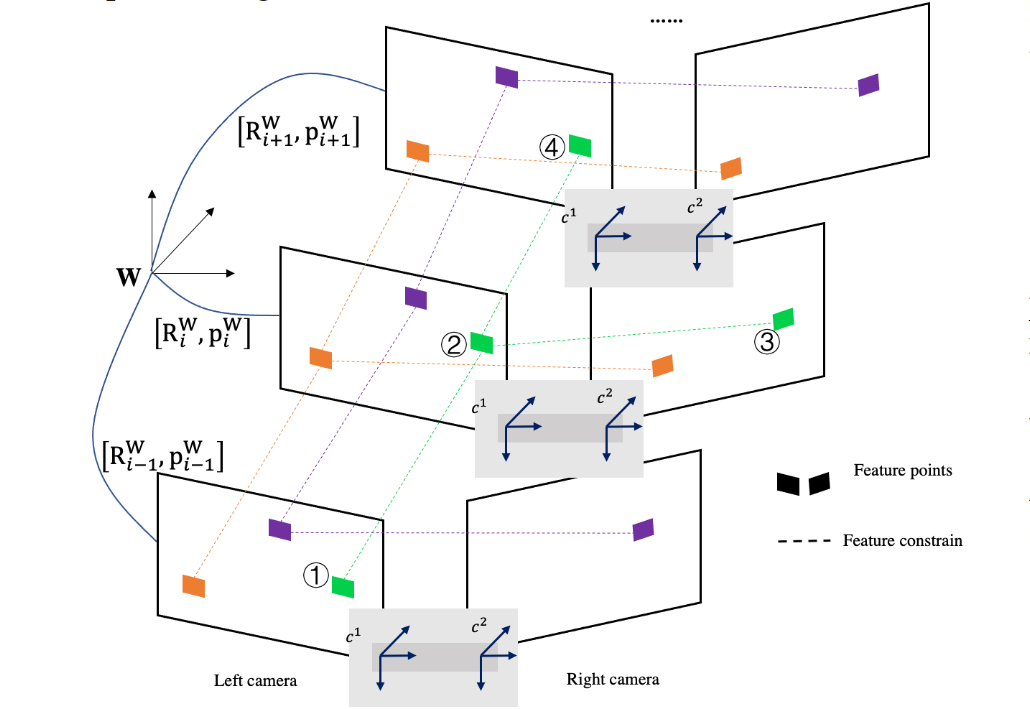
一个地标 $\mathit{P}$，其在 $\mathbf{W}$ 中的位置为 $x_p \in \mathbb{R}^3$，由多个状态观察，$\{\mathbf{S}\}_p$。它通过相机投影模型 $π(x_p):\mathbb{R}^3→\mathbb{R}^2$ 映射到图像坐标 $z = [u，v]$.假设特征（上图中的绿色）首先在第i帧中观察到，该特征在几帧中被跟踪。因此，约束函数可以写成：

$$e_{i j}=\mathrm{z}_{\mathrm{j}}-\pi\left(\mathbf{R}_{i}^{\mathrm{j}} \pi^{-1}\left(\mathrm{z}_{\mathrm{i}}\right)+\mathbf{p}_{i}^{\mathrm{j}}\right)$$

式中，$e_{ij}$ 为特征在帧 $i$ 和帧 $j -1$ 之间的重投影误差。$π(*)^{-1}:\mathbb{R}^2→\mathbb{R}^3$为 $π(*)$的倒数。$\mathbf{R}_{i}^{\mathrm{j}}$ 和 $\mathbf{p}_{i}^{\mathrm{j}}$，分别是从坐标系 $i$ 到坐标系 $j$ 的旋转和平移。

为了保证整个因子图的稀疏性，我们只使用关键帧的姿势而不是 3D 地标作为视觉因子。由于三个传感器具有不同的输出频率，并且它们不是时间同步的。为了将视觉里程计集成到系统中，我们根据激光雷达的时间戳插入虚拟视觉姿势。

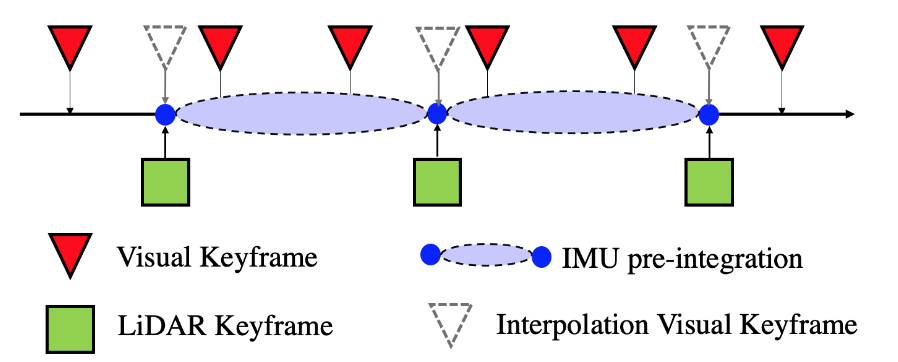
数据流转

为了进一步说明三个传感器之间的数据交互，让我们做一个简短的总结。

• 高频IMU一方面用于对激光雷达扫描进行去畸变，另一方面用于预积分，作为要添加到因子图中的预积分因子。

• 激光雷达测程是使用点到线和点到平面约束计算的。

• 在视觉测程过程中，我们提取稀疏特征点，并在空间和时间图像帧中对其进行跟踪。在滑动窗口中对三维特征点和视觉关键帧姿态进行联合优化，并具有重投影误差约束。激光雷达姿态作为三角测量过程中的初始值，以改进视觉测程优化过程。

• 然后，我们使用IMU预积分，激光雷达里程计和视觉里程计构建因子图。IMU 偏置与因子图中的激光雷达测程因子和视觉里程计因子一起优化。

实验结果

平面的一致性和对象的完整性是定位和映射质量的良好评价标准。下图显示了建筑平面图、树木和围栏的详细映射结果。我们可以清楚地区分建筑物的轮廓，树木的结构。特别是，我们可以模糊地识别每块围栏。实验结果表明，LVIO-SAM足够精确，可以重建密集的三维高精度户外环境地图。

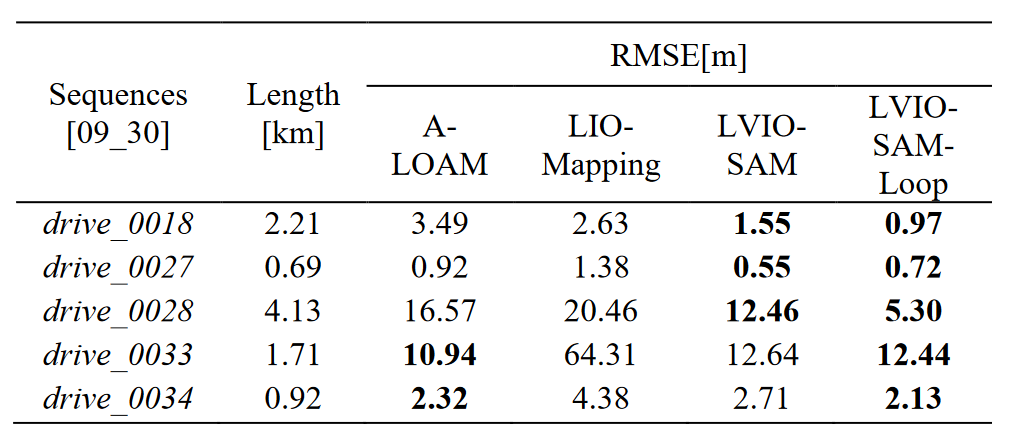
我们通过 evo 工具评估几种算法之间的 APE（绝对姿势误差）。KITTI 数据集的绝对姿势误差的 RMSE（均方根误差）显示在表中。I.对于所有序列，所提方法均显示出非常有竞争力的结果，表明LVIO-SAM在运动估计方面具有准确性。此外，闭环模块可以减少绝对位姿误差，这意味着提高轨迹估计的全局一致性。在顺序drive_0033和drive_0034中，我们发现A-LOAM和LVIO-SAM的RMSE非常接近。这个问题的可能原因是IMU内在参数，这在预积分部分非常重要，而KITTI数据集不提供。实验表明，所提方法在轨迹估计方面具有较强的竞争力。