【论文阅读：激光SLAM】 F-LOAM : Fast LiDAR Odometry and Mapping

摘要

• SLAM 在机器人领域有着广泛的应用，如自主驾驶和无人驾驶飞行器。对于一个好的SLAM系统来说，计算效率和定位精度都是非常重要的。
• 现有的基于 LiDAR 的 SLAM 的工作通常将问题表述为两个模块：Scan-to-Scan 的匹配和扫 Scan-to-Map 的细化。这两个模块都是通过迭代计算来解决的，计算成本很高。
• 在本文中，提出了一个通用的解决方案，旨在为基于 LiDAR 的 SLAM 提供一个计算高效且准确的框架
  – 采用了一种非迭代的两阶段失真补偿方法来降低计算成本
  – 对于每个扫描输入，提取边缘和平面特征并分别与局部边缘图和局部平面图相匹配，其中局部平滑度也被考虑用于迭代姿势优化。
• 它是KITTI数据集排名中最准确和最快的开源SLAM系统之一。

简介

• 同步定位和测绘（SLAM）是机器人学中最基本的研究课题之一。它的任务是在一个未知或部分未知的环境中，基于机载传感器对机器人进行定位并建立周边地图。

• 根据感知设备的不同，它可以大致分为 LiDAR 和视觉SLAM。与视觉SLAM相比，LiDAR SLAM在姿态估计方面通常更加准确，并且对环境变化如光照和天气变化具有鲁棒性

• 因此，LiDAR SLAM被许多机器人应用广泛采用，如自主驾驶、无人机检查和仓库操作。尽管现有的LiDAR SLAM的工作在公共数据集评估中取得了良好的性能，但在实际应用中仍有一些局限性。
  – 其中一个限制是对不同环境的鲁棒性，例如从室内到室外环境，从静态到动态环境。
  – 另一个挑战是计算成本。在许多机器人平台（如无人机）中，计算资源是有限的，机载处理单元应该同时执行高频定位和路径规划

• 最经典的估计两个扫描之间的变换的方法是迭代最接近点（ICP），其中两个扫描通过最小化点云距离来迭代对齐。然而，大量的点涉及到优化，这在计算上是低效的。

• 另一种方法是匹配特征，在计算上更有效率。一个典型的例子是激光雷达测绘（LOAM），它提取边缘和平面特征，并通过最小化点到平面和点到边缘的距离来计算姿势。
  – 然而，失真补偿和激光位置估计都需要迭代计算，这在计算上仍然很昂贵。

在本文中，介绍了一个轻量级的激光雷达SLAM，旨在为公众提供一个实用的实时激光雷达SLAM解决方案。本文提出了一个新颖的框架，将特征提取、失真补偿、姿势优化和建图结合起来。与传统方法相比，我们使用非迭代的两阶段失真补偿方法来取代计算效率低下的迭代失真补偿方法。

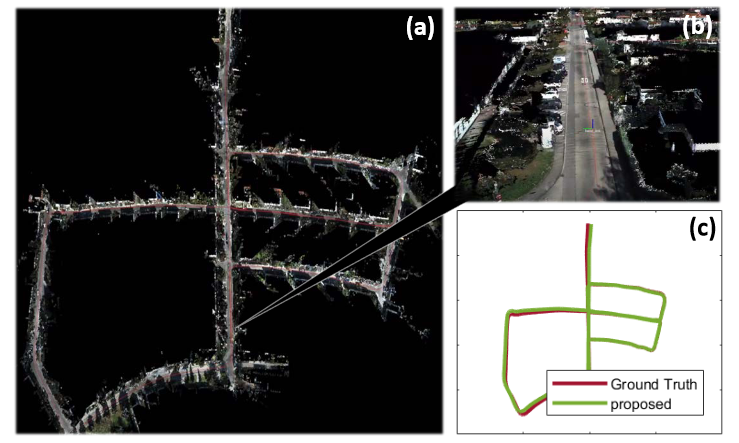
据观察，在连续的扫描中，局部平滑度较高的边缘特征和平滑度较低的平面特征往往被持续提取。这些点对匹配更为重要。因此，局部几何特征也被考虑用于迭代姿势估计以提高定位精度。它能够在一个低功率的嵌入式计算单元上实现高达20赫兹的实时性能。

相关工作

LiDAR SLAM中最重要的步骤是点云匹配，包括两大类：原始点云匹配和特征点对匹配

对于原始点云匹配，迭代最接近点（ICP）方法是最经典的方法。

• ICP 通过寻找欧氏空间中最接近的点来测量对应的点。通过迭代最小化对应点之间的距离残差，两个点云之间的姿势转换会收敛到最终位置。
• 一种改进的点云匹配是IMLS-SLAM[9]，其中为每个点分配一个权重值。每个权重都是由IMplicit Least Square (IMLS) 方法根据目标点的局部表面法线得出。
• 然而，应用原始点云匹配计算成本通常很高，例如，在IMLSSLAM中估计一帧需要1.2秒，这与实时性能要求相差甚远。

基于特征的方法主要是利用点-面/边的匹配，并被广泛使用。

• 由 LOAM 引入，这已成为以下工作的标准。边缘和表面是基于局部平滑度分析预先提取的，当前点云中的点与地图中的边缘和表面进行匹配。距离成本被表述为点与边缘和表面之间的欧几里得距离。
• 也有很多作品对LOAM进行了扩展，以达到更好的性能，例如 LeGO-LOAM 在特征提取之前就分离了地面优化。
  – 对于自主导航车辆（AGVs），Z轴并不重要，大多数情况下，我们可以假设机器人在二维空间移动。因此，地面点对X-Y平面的定位没有贡献。这种方法也被广泛地应用于地面车辆。
• 一些工作试图通过引入额外的模块来提高性能。环路闭合检测是SLAM的另一个关键组成部分。LiDAR位姿估计经常伴随着不可避免的漂移，这在长期的SLAM中可能是很重要的。
  – 因此，在一些大规模的场景中，环路闭合在后端用于识别重复的地方。例如，在LiDAR-only Odometry and Localization (LOL)中，扩展为具有循环闭合功能的完全SLAM。通过闭环，可以纠正位姿的漂移误差。

不同的传感器输入被同步和紧密地耦合在一起。融合后的SLAM系统被证明在户外环境中比LOAM更准确。基于融合的方法已经显示出对定位精度的改善。

• 与惯性测量单元（IMU）的融合是一种替代解决方案。Shan等人提出了一种融合IMU和GPS的方法，名为LIO-SLAM。
• 然而，多传感器融合需要同步和全面校准

在过去的几年里，也有一些基于深度学习相关的工作，试图使用卷积神经网络（CNN）进行点云处理。

• 与其说是手工制作的特征，不如说是通过 CNN 训练提取的特征。
• 例如，在 CAE-LO 中，作者通过无监督的卷积自动编码器（CAE）提出了一个基于深度学习的特征点选择规则，而 LiDAR 的位姿估计仍然是基于特征点匹配。
  – 实验结果表明，学习到的特征可以提高匹配的成功率。
  – 尽管深度学习方法在公共数据集中表现出良好的性能，但在室内/室外和城市/农村等不同环境中并不稳健。
  – 然而，当转移到室内环境或一些复杂的环境中时，同样的算法就会失效。

方法论

在这一节中。首先介绍了传感器模型和特征提取。然后用失真补偿对提取的特征进行标定。然后，我们介绍一般的特征提取和全局特征估计。最后，我们解释了激光位姿估计以及建图的计算。

A：传感器模型和特征提取

机械式三维激光雷达通过旋转数量为 $M$ 的垂直排列的激光束阵列来感知周围环境。它以 $M$ 个读数平行地扫描垂直平面。在每个扫描间隔期间，激光阵列在水平面上以恒定的速度旋转，而激光测量则按顺时针或逆时针的顺序依次进行。对于机械LiDAR传感器模型，我们将第 $k$ 次LiDAR扫描记为 $P_k$ ，每个点记为 $\mathbf{p}_k^{(m, n)}$ ，其中 $m∈[1, M]，n∈[1, N]$。

原始点云匹配方法，如ICP，对噪声和动态物体（如自动驾驶的人类）很敏感。此外，一个LiDAR扫描包含数万个点，这使得 ICP 的计算效率很低。与 ICP 等原始点云匹配方法相比，

特征点匹配在实践中更加稳健和高效。为了提高匹配精度和匹配效率，我们利用了表面特征和边缘特征，同时抛弃了那些有噪声或不太重要的点。

三维机械激光雷达返回的点云在垂直方向是稀疏的，在水平方向是密集的。因此，水平方向的特征更加明显，在水平方向上出现错误特征检测的可能性较小。

对于每个点云，我们关注水平面，并通过以下方式评估局部表面的平滑度：

$$\sigma_k^{(m, n)}=\frac{1}{\left|\mathcal{S}_k^{(m, n)}\right|} \sum_{\mathbf{p}_k^{(m, j)} \in \mathcal{S}_k^{(m, n)}}\left(\left\|\mathbf{p}_k^{(m, j)}-\mathbf{p}_k^{(m, n)}\right\|\right)$$

其中 $\mathcal{S}_k^{(m, n)}$ 是 $\mathbf{p}_k^{(m, n)}$ 在水平方向上的相邻点， $|\mathcal{S}_k^{(m, n)}|$ 是本地点云中的点的数量。$\mathcal{S}_k^{(m, n)}$ 可以很容易地根据点的ID $n$ 来收集，与本地搜索相比，它可以减少计算成本。

在实验中，我们沿顺时针和逆时针分别选取5个点。对于平坦的表面如墙壁，平滑度值很小，而对于角落或边缘点，平滑度值很大。对于每个扫描平面 $P_k$ 来说，边缘特征点选择的是高 $σ$，而表面特征点选择的是低 $σ$ 。因此，我们可以将边缘特征集表述为 ${\mathcal{E}}_k$，表面特征集表述为 $S_k$。

B：运动估计和失真补偿

在现有的工作中，如 LOAM 和 LeGO-LOAM，失真是通过 Scan-to-Scan 的匹配来纠正的，这种匹配反复估计两个连续激光扫描之间的变换。然而，迭代计算需要找到转换矩阵，这在计算上是低效的。

在本文中，我们建议使用两阶段的失真补偿来减少计算成本。请注意，大多数现有的三维激光雷达能够以超过10赫兹的速度运行，而且两个连续的激光雷达扫描之间的时间往往非常短。

1、在第一阶段，首先可以假设在短时间内角速度和线速度恒定，以预测运动和纠正失真。
2、在第二阶段，在姿态估计过程中，失真将被重新计算，重新计算的未失真特征将被更新到最终地图。

在实验中我们发现，两阶段的失真补偿可以达到类似的定位精度，但计算成本要低得多。

第一阶段

基于前面的假设，将机器人在第 $k$ 次扫描时的姿势表示为一个 $4x4$ 的变换矩阵 $T_k$，两个连续帧 $k-1$ 和 $k$ 之间的6-DoF变换可以通过以下方式估计：

$$\xi_{k-1}^k=\log \left(\mathbf{T}_{k-2}{ }^{-1} \mathbf{T}_{k-1}\right)$$

其中 $ξ∈se(3)$。连续扫描之间的小周期 $δt$ 的变换可以通过线性插值估计：

$$\mathbf{T}_k(\delta t)=\mathbf{T}_{k-1} \exp \left(\frac{N-n}{N} \xi_{k-1}^k\right)$$

其中，函数 $exp(ξ)$ 将李代数转换为李群。当前扫描 $P_k$ 的失真可以通过以下方式进行修正：

$$\tilde{\mathcal{P}}_k=\left\{\mathbf{T}_k(\delta t) \mathbf{p}_k^{(m, n)} \mid \mathbf{p}_k^{(m, n)} \in \mathcal{P}_k\right\}$$

未失真的特征将在下一节用于计算机器人的姿势。

C：位姿估计

姿势估计将当前未扭曲的边缘特征 $\tilde{\mathcal{E}}_k$ 和平面特征 $\tilde{\mathcal{S}}_k$ 与全局特征图对齐。全局特征图由一个边缘特征图和一个平面特征图组成，它们被分别更新和维护。为了减少搜索的计算成本，边缘和平面图都存储在3D KD树中。

全局线和平面是通过收集边缘和平面特征图的附近点来估计的。

• 对于每个边缘特征点 $\mathbf{p}_\mathcal{E} \in \tilde{\mathcal{E}}_k$，我们从全局边缘特征图中计算其附近点的协方差矩阵。当这些点分布在一条线上时，协方差矩阵包含一个很大的特征值。与最大特征值相关的特征向量 $\mathbf{n}_{\mathcal{E}}^g$ 被认为是线的方向，线 $\mathbf{p}_{\mathcal{E}}^g$ 的位置被当作附近点的几何中心。
• 同样，对于每个平面特征点 $\mathbf{p}_{\mathcal{E}} \in \tilde{\mathcal{S}}_k$，我们可以得到一个全局平面，其中位置 $\mathbf{p}_{\mathcal{S}}^g$ 和表面法向量 $\mathbf{n}_{\mathcal{S}}^g$。需要注意的是，与全局边缘不同，全局平面的法向量被认为是与最小特征值相关的特征向量。

当得出相应的最优边/平面，我们就可以从 $\tilde{\mathcal{P}}_k$ 中为每个特征点找到相关的全局边或平面。这种对应关系可用于通过最小化特征点和全局边缘/平面之间的距离来估计当前帧和全局图之间的最佳姿态。边缘特征与全局边缘之间的距离为：

$$f_{\mathcal{E}}\left(\mathbf{p}_{\mathcal{E}}\right)=\mathbf{p}_{\mathbf{n}} \bullet\left(\left(\mathbf{T}_k \mathbf{p}_{\mathcal{E}}-\mathbf{p}_{\mathcal{E}}^g\right) \times \mathbf{n}_{\mathcal{E}}^g\right)$$

其中符号 $\bullet$ 是点乘，$\mathbf{p}_{\mathbf{n}}$是单位向量，由以下公式给出：

$$\mathbf{p}_{\mathbf{n}}=\frac{\left(\mathbf{T}_k \mathbf{p}_{\mathcal{E}}-\mathbf{p}_{\mathcal{E}}^g\right) \times \mathbf{n}_{\mathcal{E}}^g}{\left\|\left(\mathbf{T}_k \mathbf{p}_{\mathcal{E}}-\mathbf{p}_{\mathcal{E}}^g\right) \times \mathbf{n}_{\mathcal{E}}^g\right\|}$$

平面特征与全局平面之间的距离：

$$f_{\mathcal{S}}\left(\mathbf{p}_{\mathcal{S}}\right)=\left(\mathbf{T}_k \mathbf{p}_{\mathcal{S}}-\mathbf{p}_{\mathcal{S}}^g\right) \cdot \mathbf{n}_{\mathcal{S}}^g$$

传统的特征匹配只优化了上述的几何距离，而没有考虑每个特征点的局部几何分布。然而，据观察，局部平滑度较高的边缘特征和平滑度较低的平面特征往往在连续的扫描中被持续提取，这对匹配更为重要。因此，引入了一个权重函数来进一步平衡匹配过程。为了降低计算成本，之前定义的局部平滑度被重新用于确定权重函数。对于每个边缘点 点 $\mathbf{p}_{\mathcal{E}}$ 的局部光滑度为 $\sigma_{\mathcal{E}}$，每个平面点 $\mathbf{p}_{\mathcal{S}}$ 的局部光滑度为 $\sigma_{\mathcal{S}}$，其权重定义为：

$$\begin{aligned} & W\left(\mathbf{p}_{\mathcal{E}}\right)=\frac{\exp \left(-\sigma_{\mathcal{E}}\right)}{\sum_{\mathbf{p}^{(i, j)} \in \tilde{\mathcal{E}_k}} \exp \left(-\sigma_k^{(i, j)}\right)} \\ & W\left(\mathbf{p}_{\mathcal{S}}\right)=\frac{\exp \left(\sigma_{\mathcal{S}}\right)}{\sum_{\mathbf{p}^{(i, j)} \in \overline{\mathcal{S}_k}} \exp \left(\sigma_k^{(i, j)}\right)}, \end{aligned}$$

其中 $\mathcal{E}_k$ 和 $\mathcal{S}_k$ 是 $k^{t h}$ 扫描的边缘特征和平面特征。新的姿态是通过最小化点到边缘和点到平面距离的加权和来估计的：

$$\min _{\mathbf{T}_k} \sum W\left(\mathbf{p}_{\mathcal{E}}\right) f_{\mathcal{E}}\left(\mathbf{p}_{\mathcal{E}}\right)+\sum W\left(\mathbf{p}_{\mathcal{S}}\right) f_{\mathcal{S}}\left(\mathbf{p}_{\mathcal{S}}\right) .$$

通过高斯-牛顿法求解非线性方程，可以得出最佳姿势估计。Jacobian可以通过应用左扰动模型$delta \xi \in \mathfrak{s e}(3)[20]$来估计：

$$\begin{aligned}\mathbf{J}_p=\frac{\partial \mathbf{T} \mathbf{p}}{\partial \delta \xi} & =\lim _{\delta \xi \rightarrow \mathbf{0}} \frac{(\exp (\delta \xi) \mathbf{T} \mathbf{p}-\mathbf{T} \mathbf{p})}{\delta \xi} \\ & =\left[\begin{array}{cc}\mathbf{I}_{3 \times 3} & -[\mathbf{T} \mathbf{p}]_{\times} \\\mathbf{0}_{1 \times 3} & \mathbf{0}_{1 \times 3}\end{array}\right],\end{aligned}$$

其中 $\left[\mathbf{T}_k \mathbf{p}_k\right]_{\times}$ 将4D点表达式 $\{x, y, z, 1\}$ 转换成3D点表达式 $\{x, y, z\}$ 并计算其倾斜对称矩阵。边缘残差的雅各布矩阵可以通过以下方式计算：

$$\mathbf{J}_{\mathcal{E}}=W\left(\mathbf{p}_{\mathcal{E}}\right) \frac{\partial f_{\mathcal{E}}}{\partial \mathbf{T} \mathbf{p}} \frac{\partial \mathbf{T} \mathbf{p}}{\partial \delta \xi}=W\left(\mathbf{p}_{\mathcal{E}}\right) \mathbf{p}_{\mathbf{n}} \cdot\left(\mathbf{n}_{\mathcal{E}}^g \times \mathbf{J}_p\right),$$

类似地，我们可以推导出

$$\mathbf{J}_{\mathcal{S}}=W\left(\mathbf{p}_{\mathcal{S}}\right) \frac{\partial f_{\mathcal{S}}}{\partial \mathbf{T} \mathbf{p}} \frac{\partial \mathbf{T} \mathbf{p}}{\partial \delta \xi}=W\left(\mathbf{p}_{\mathcal{S}}\right) \mathbf{n}_{\mathcal{E}}^g \cdot \mathbf{J}_p .$$

通过求解非线性优化，我们可以得出基于上述对应关系的里程计估计。然后，我们可以用这个结果来计算新的对应关系和新的测距。当前的姿态估计 $\mathbf{T}^*_k$ 可以通过迭代姿态优化来解决，直到它收敛。

D：地图构建与失真补偿更新

全局地图由一个全局边缘地图和一个全局平面地图组成，并根据关键帧进行更新。当平移变化大于预定的平移阈值，或旋转变化大于预定的旋转阈值时，每个关键帧被选中。与逐帧更新相比，基于关键帧的地图更新可以减少计算成本。

如第B节所述，为了降低计算成本，失真补偿是基于恒定速度模型而不是迭代运动估计进行的。然而，这比LOAM中的迭代失真补偿要不准确。因此，在第二阶段，根据上一步的优化结果T∗ k重新计算失真，即：

$$\begin{gathered} \Delta \xi^*=\log \left(\mathbf{T}_{k-1}^{-1} \cdot \mathbf{T}_k^*\right) \\ \tilde{\mathcal{P}}_k^*=\left\{\exp \left(\frac{N-n}{N} \cdot \Delta \xi^*\right) \mathbf{p}_k^{(m, n)} \mid \mathbf{p}_k^{(m, n)} \in \mathcal{P}_k\right\} \end{gathered}$$

重新计算的未扭曲边缘特征和平面特征将分别更新到全局边缘图和全局平面图。每次更新后，为了防止内存溢出，地图会通过三维体素化网格方法进行降采样。

补充：

ξ∈se(3) 的含义与数学意义：

在机器人定位和运动中，符号 $ξ∈se(3)$ 表示一个在三维特殊欧几里德群（Special Euclidean Group）上的李代数。具体来说，$ξ$ 是一个6维向量，其中前三个元素表示平移分量（x、y、z），后三个元素表示旋转分量（绕x、y、z轴的旋转）。

一个例子是，考虑一个机器人在三维空间中的运动。假设 $ξ=[0.1, 0.2, 0.3, 0, 0, 0.1]$，其中前三个元素表示机器人在x、y、z方向上的平移距离为[0.1, 0.2, 0.3]，后三个元素表示机器人绕x、y、z轴的旋转分别为0弧度，0弧度和0.1弧度。

这个 $ξ$ 向量可以用于描述机器人的相对位姿变换，例如从一个位置移动到另一个位置的相对运动。通过将 $ξ$ 向量与初始位姿进行组合，可以得到机器人在新位姿下的姿态。

需要注意的是，李代数 $se(3)$ 中的元素可以通过李代数的指数映射（exponential mapping）转换为特殊欧几里德群SE(3)中的变换矩阵，也可以通过对数映射（logarithmic mapping）将特殊欧几里德群 $SE(3)$ 中的变换矩阵转换为李代数 $se(3)$ 中的向量。这种转换在机器人定位和运动估计中经常用到。