侧边栏壁纸
博主头像
郑育

  • 累计撰写 131 篇文章
  • 累计创建 16 个标签
  • 累计收到 4 条评论
标签搜索

目 录CONTENT

文章目录
机器学习   

深度强化基础内容学习

什么是深度强化学习

深度强化学习(Deep reinforcement learning)是机器学习的子领域，利用深度学习模型来解决强化学习中的任务。

就深度学习而言，其也是机器学习的一个分支，例如用来图像分类，就是实现一个函数在输入图片后预测输出分类标签，这个函数有一个可调的参数模型，在初始条件下，这些参数是随机值，所以不管输入什么，输出都是一个随机标签。然后通过数据集对模型迭代训练，不断调整参数来逼近真实标签。

深度神经网络所以大受欢迎，因为大多时候其能够最精确地描述给定任务的参数模型。这得益于其数据表示方法，在深度神经网络中存在许多的隐藏层，这些层对输入的数据进行分层学习，即将数据表示为更简单数据的组合。

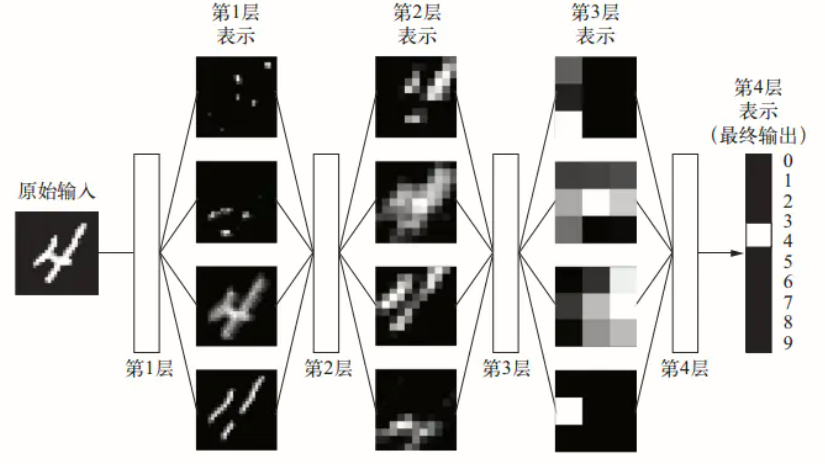
对于强化学习更重要的是学会如何做出动作决策，完成既定的控制任务。其中我们可以自由的选择有效算法来实现控制任务。深度神经网络能够有效地表达复杂数据模型，这就是为深度强化学习为什么大受欢迎。

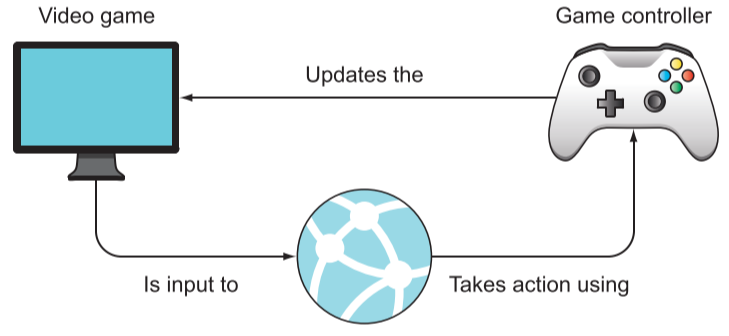
从图像处理到控制任务的额外复杂度就是时间，而在图像处理中通常不考虑时间的连续性问题。在控制任务中每一条数据都是时空上的连续，且后面的数据往往受前面数据的影响。

通常的图像处理任务是监督学习，模型训练过程需要提供一系列的图片与对应标签，模型开始时进行随机猜测，并进行迭代校正，直到学习到图像中与适当标签相对应的特征。

与之相反，强化学习并不知道每一步怎么做是正确的，只是知道最终目标和规则。在训练过程中，如果它完成了既定任务，我们基于奖励，如果违反规则，则给予惩罚。整个训练过程是在模拟器中完成，让模型在不断尝试中学习如何避免失败与惩罚，尽量最大化奖励。

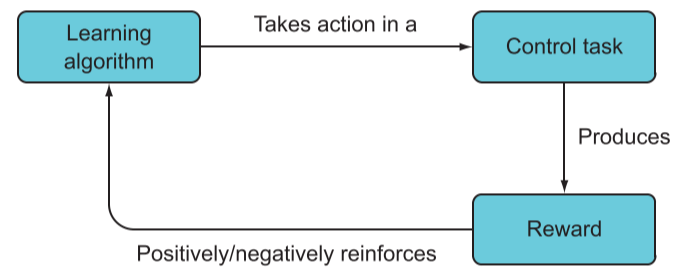
动态规划与蒙特卡洛

动态规划通过将复杂的高级问题分解为越来越小的子问题来解决，直到得到一个无需进一步分解即可解决的简单子问题。但是在强化学习中我们很难将问题如此分解，经常遇到可能包含一些随机情况，不能完全应用动态规划。

蒙特卡洛方法本质上是从环境中随机抽样，通过不断的试错来了解环境来解决问题。

强化学习基础框架

强化学习标准模型包括：智能体、环境、动作空间、状态空间、奖励。

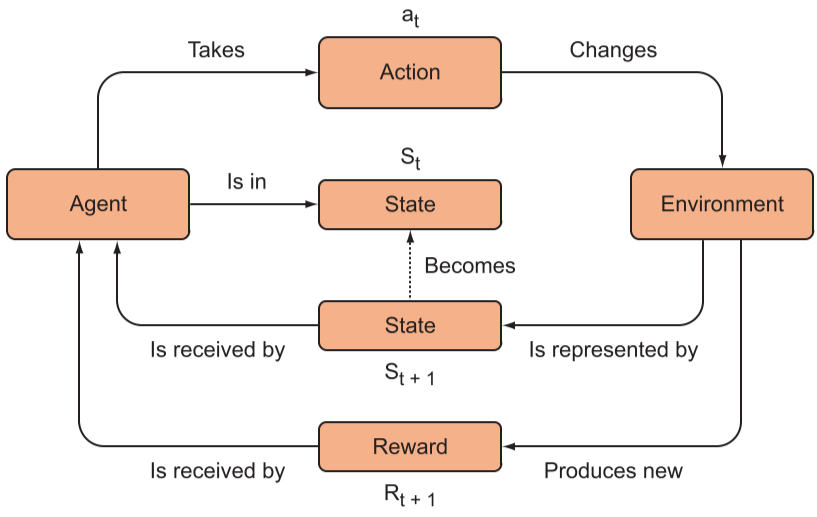
从智能体的视角来解释框架，首先智能体从环境中获取所需的状态空间变量输入自身的模型中，输出动作空间中的一个动作，改变环境并收到一个奖励反馈（包括正或负）。

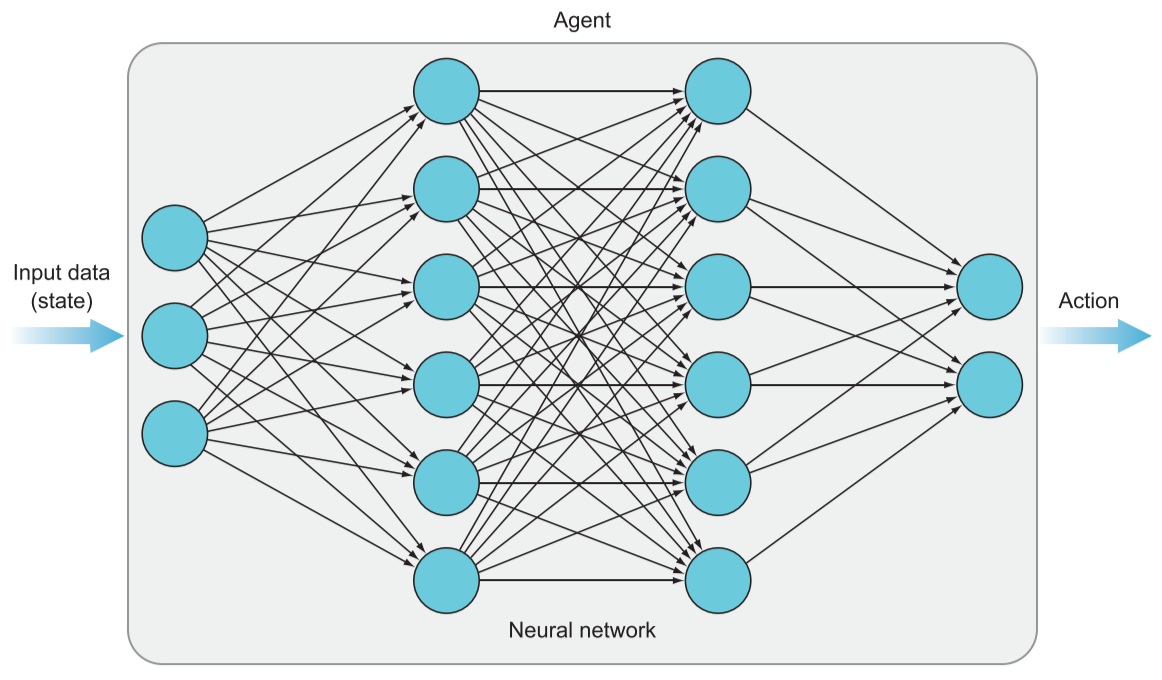
马尔可夫决策过程

多老虎机问题

假设现在有四台老虎机，不需要投币，只需要摇动摆臂就能获得 0 到 10 元的随机奖励，但是每台的平均奖励值是不同的，如果我们可以玩的次数有限，如何获取最大奖励。

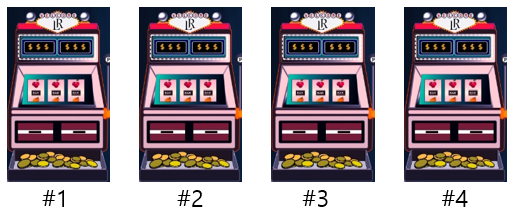
将问题可以简化为，我们有 4 个可能的动作空间（action space），即选择哪一个老虎机来玩。当我们做出决定并动作（action）后，收到一个奖励反馈（reward）。

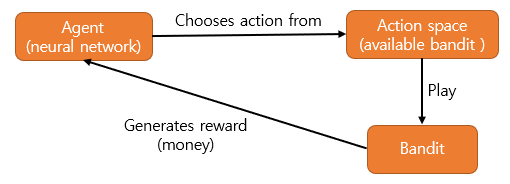
我们的游戏策略应该是，首先尝试不同的老虎机玩几把，观察返回的奖励分布，之后选择平均奖励最高的老虎机一直玩。根据之前玩的经验，这时我们会有一个预期过程，即当前的动作会获得多少奖励的预期。在数学上，我们将这个预期过程建立为预期函数Qk(a)，也称为价值函数Q。

以上过程可以分为探索和开发两个阶段。探索时，我们只是随机的选取动作，并观察奖励，而开发时，则是根据先前经验选择可能最多的奖励动作来执行。

广告投放问题

假设你是某购物网站的策划，你有许多不同类型的产品，你希望在不同的页面投放一个广告来吸引客户点击。

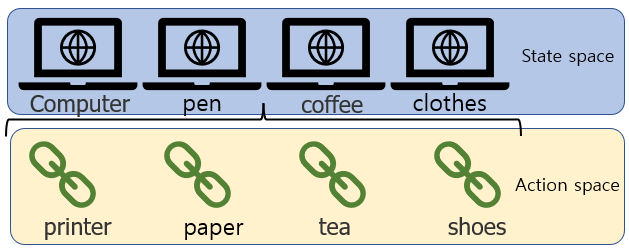
问题可以简化为，在不同的状态空间（state spaces，不同网站）中执行动作空间（action space，不同广告）的某个动作，并获取奖励反馈（reward，点击量）。

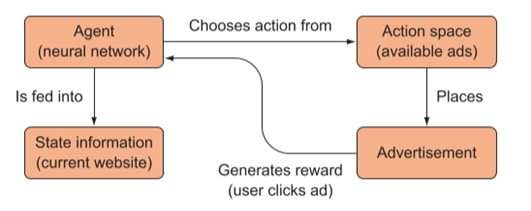
意味着，状态空间中每个状态和动作空间中的每个动作都会有其单独的关系，我们称为状态-动作对（state-action pair (s, a)）。也就是说，状态-动作对的数量是关于状态空间和动作空间所倍数增长的，这也是为什么我们需要用深度网络来描述模型了。

马尔可夫性质

从前面的定义和例子中可以看到，深度神经网络的输入是当前状态，根据当前的状态产生预期奖励并选择最佳动作。这是强化学习中的一个重要属性，称为马尔可夫属性。表现出马尔可夫属性的任务被称为马尔可夫决策过程（Markov decision process，MDP）。

对于 MDP 而言，当前状态就包含足够的信息来选择最佳动作以最大化未来的奖励。MDP 模型极大地简化了 RL 问题，因为我们不需要采取考虑到所有以前的状态或动作，我们只需要分析当前状态。

当然不是所有的任务天然具有马尔可夫性质，但是我们还是可以通过更多信息加入当前状态，进而有效地诱导出马尔可夫性质。例如马里奥游戏中我们可以将最近的5帧认为是当前状态，学习到怪物是在靠近马里奥还是远离，从而做出更有效判断。

Deep Q-learning Network（DQN）

Q-learning

传统的 Q-learning 的主要思想是算法预测一个状态-动作对的值，然后你将这个预测与观察到的奖励进行比较，并更新算法的参数，以便下次做出更好的预测。其中 Q-learning 并不是预测在采取特定行动后将获得的奖励，它是在预测期望值（期望奖励），这是我们在一个状态下采取动作所获得的长期平均奖励。

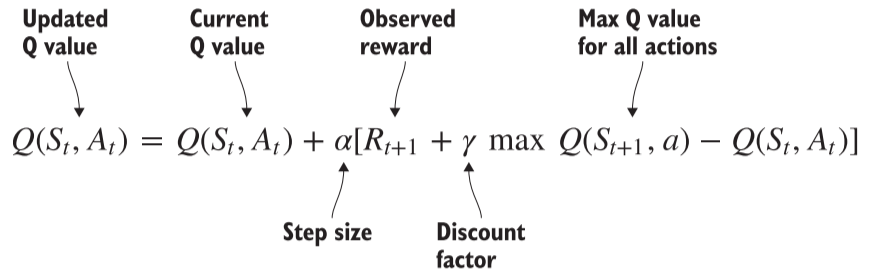
参数 α 称为学习率，它控制着算法学习每一步的速度，小的值意味着每次进行一小步更新。

参数 γ 称为折现率，它控制智能体在做出决策时对未来奖励的折扣程度。也就是认为当前的奖励和未来奖励的相等性比例，例如现在得到100元和下个月得到200元具有相等性，则折现率为 100/200=0.5。

Deep Q-learning Network

而在 DQN 简化了原来的 Q-learning 接受一个状态-动作对并返回该状态-动作对的值，直接接受一个状态并返回该状态-动作对的值向量，

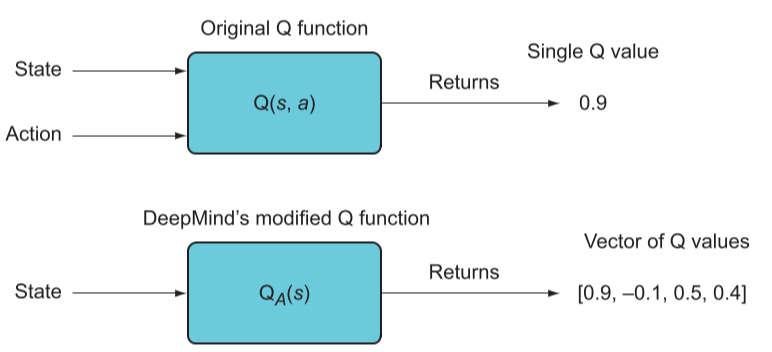
其网络结构如下，其输入层是状态的一维展开，而输出层则是对应的状态-动作空间的值。

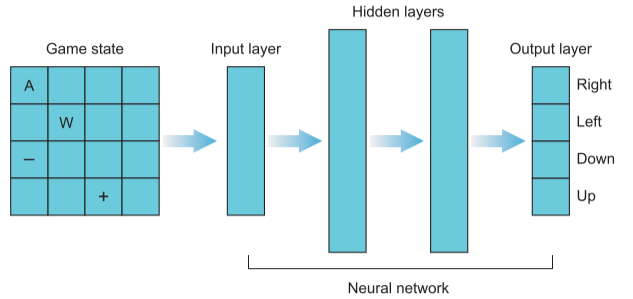
经验回放

在训练 DQN 时，如果我们将每一次动作直接进行训练，我们会发现一个问题，当环境状态变化时，相同的动作在前后所获得的奖励相反，这可能会覆盖之前的训练，DQN 变的疑惑。所以我们通常采取经验回放法来训练 DQN

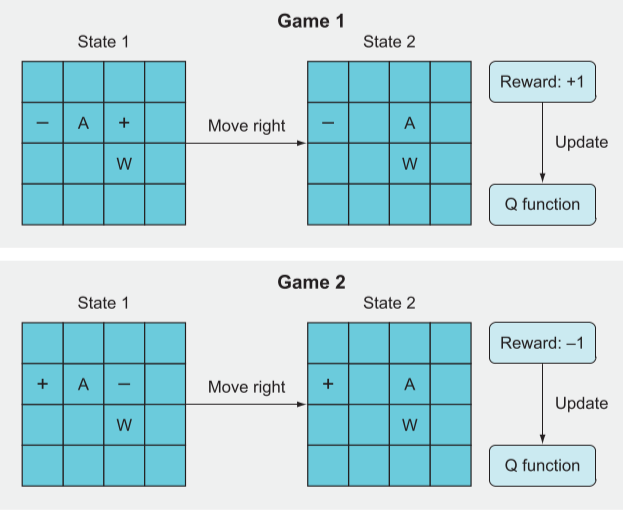
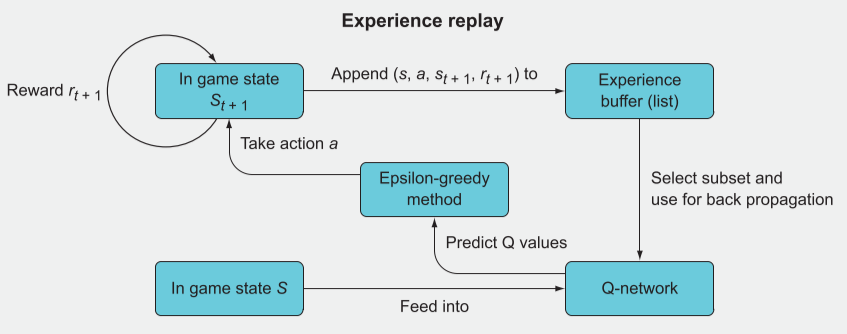
经验回放法就是实现批量更新，流程为：

  • 在状态s，采取行动a，观察新状态st+1，奖励rt+1。
  • 这时不进行训练，而是将(s, a, st+1, rt+1)作为经验元组储存在列表中。
  • 将每个经验存储在此列表中，直到将列表填充到特定长度。
  • 当经验列表被填满后，随机选择一个子集。
  • 遍历子集并计算目标 Q 值（Y）与当前 Q 值（X）。
  • 使用 X 和 Y 批量训练。 对后续的数据则进行压栈处理。

提高训练稳定性

如果在每次动作后都对 DQN 网络进行更新，会发现损失图极为不稳定比较震荡，这是由于奖励是稀疏的，而且有时候动作与奖励是相反的，预测的 Q值 永远不会稳定在一个合理的值上。

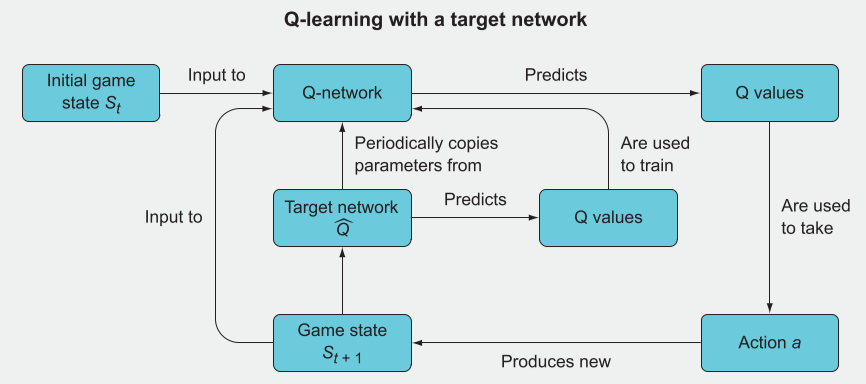
采用一种延迟的方法来实现训练的稳定，流程如下：

  • 共同初始化 Q-network 和 Target network 为相同参数。
  • 使用带有 Q-network 的 Q值 来选择动作 a。
  • 观察奖励和新状态 rt+1,St+1。
  • Target network 的 Q值 将设置为 rt+1（游戏结束） 或 rt+1 + γmaxQθr(St+1)
  • 利用 Target network 的 Q值 对 Q-network 进行反向传播，更新网络。
  • 每 C 次迭代，将 Target network 的参数等于 Q-network 的参数。

策略梯度法（Policy gradient methods）

在 DQN 中输入状态值(state)，输出 Q值，再基于策略选择动作(action)。

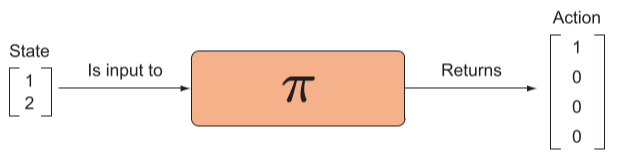
将神经网络作为策略网络

现在希望智能体的网络能够直接输出动作，将策略的选择也整合到网络中形成策略网络，更准确的说是，将返回动作的离散概率分布，进而从这个分布中采样来选择动作。最有效动作将最有可能从随机抽样中被选中，因为它们被分配了最高概率。

随机策略网络

在随机性策略网络中，输出是是一个动作向量，表示概率分布。当然，在模型初始化的时候，每个动作概率应该是近似相等的。

当环境稳定，即状态和奖励的分布是恒定的，也可使用确定性策略，将期望概率分配给单个结果的分布。但是即使环境稳定，我们也很少采用这个，因为它无法正确的探索，难以建立神经网络模型。

建立目标函数

对于 DNQ 网络来说，我们采用了 MSE 损失函数来优化网络，用的是 Q值 和 期望Q值，这与通常的监督学习网络训练方法相同，都是基于预测值与真实值的关系。当进行前向计算，网络参数是固定的，而输入参数是变化的。当进行反向传播时，相对于固定输入改变网络参数，以找到一组参数来优化我们目标函数。

但是对于策略网络则是不同，其输出的是动作空间的概率分布，在采取动作更新之后，没有明显的方法来映射我们观察到的奖励。所以在策略网络中的训练形式不同于 DQN 。

在我们执行了某个动作后，发现获得奖励，意味着我们需要加强该动作在该状态下的概率，因为总体概率之和为1，所以加强其中一个的概率，则其他的将被减弱。

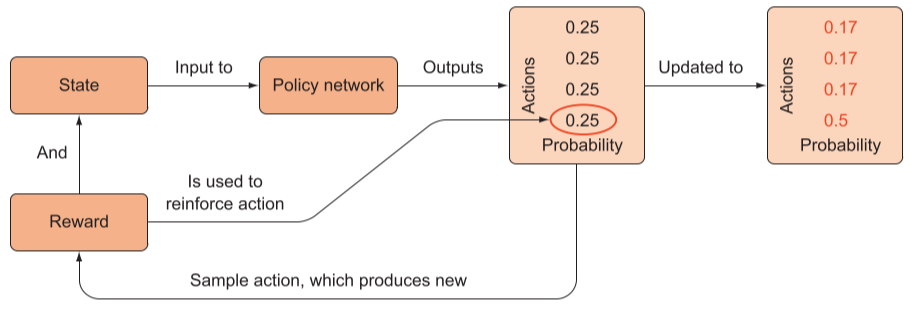
其目标函数我们表达为：πs(a∣θ)\pi_{s}(a|\theta)。意思是在某状态下，调整网络参数 θ\theta 来加强动作 a 的概率。也即是最大化 πs(a∣θ)\pi_{s}(a|\theta)。

一般在 Pytorch 中我们习惯将目标函数最小化，所以将其变形为：1−πs(a∣θ)1-\pi_{s}(a|\theta)。

在数学优化时 1−πs(a∣θ)1-\pi_{s}(a|\theta) 限制了 πs(a∣θ)\pi_{s}(a|\theta) 范围在 0-1 之间，当数值接近 1 或 0 时，变化幅度小。通常我们将其处理为：1−log⁡πs(a∣θ)1-\log \pi_{s}(a \mid \theta)。这样πs(a∣θ)\pi_{s}(a|\theta) 就获得了极大的动态范围，并且可以运用对数运算法。

贡献分配（Credit assignment）

对于整场游戏而言，有许多个动作，但动作之间的重要程度是不同的。通常我们认为，越是接近终点的动作越是重要。所以需要对损失函数加以折扣系数，定义为：

−γt∗Gt∗log⁡πs(a∣θ)-\gamma_{t} * G_{t} * \log \pi_{s}(a \mid \theta)

  • γt\gamma_{t} 是折扣系数，下标 t 将取决于时间步长，比最近的动作更折扣更远的动作。
  • GtG_{t} 是时间步 t 的总奖励，是从开始到结束收集的奖励之和。

训练模型

在策略网络训练时，输入的是一整轮的数据，即智能体开始执行动作到结束游戏的一轮，再通过更新参数来训练策略网络以最小化目标（即损失）函数。

  • 计算每个时间步实际采取的动作的概率。
  • 将概率乘以折扣回报（奖励的总和）。
  • 使用这个概率加权回报来反向传播并最小化损失。

Distributed Advantage Actor-critic 模型（DA2C）

DA2C 结合了 DQN 的在线学习优势，和策略网络的直接输出动作概率分布优势。在多领域为 state-of-the-art 结果。

结合 DQN 和 策略

DQN 能够直接从奖励中在线学习，学会了预测奖励，采用高预测的动作。

策略网络则是通过强化获得积极奖励的行为，抑制获得负面奖励的行为。

损失函数

结合两者的优点，以策略网络为基础，通过加入 DQN 的特性来提高整体的稳健性：

  • 通过更加频繁的模型更新来提高样本的效率
  • 减少用于更新模型的奖励的方差
    这些问题是相关的，因为奖励方差取决于样本量（更多样本产生更少的方差）。 DA2C 背后的想法是使用 DQN 来减少用于训练策略的奖励方差。 也就是说，不是最小化包含直接参考观察到的奖励 R 的强化损失，而是添加一个基线值，使得现在的损失为：

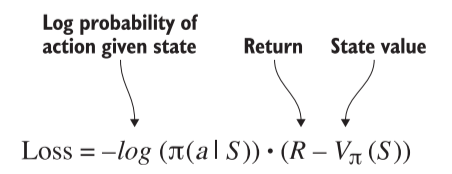
这里，V(S)V(S) 是状态 SS 的值，它是状态值函数。V(S)–RV(S) – R，被称为优势，是动作相对于预期的优势量。

模型建立

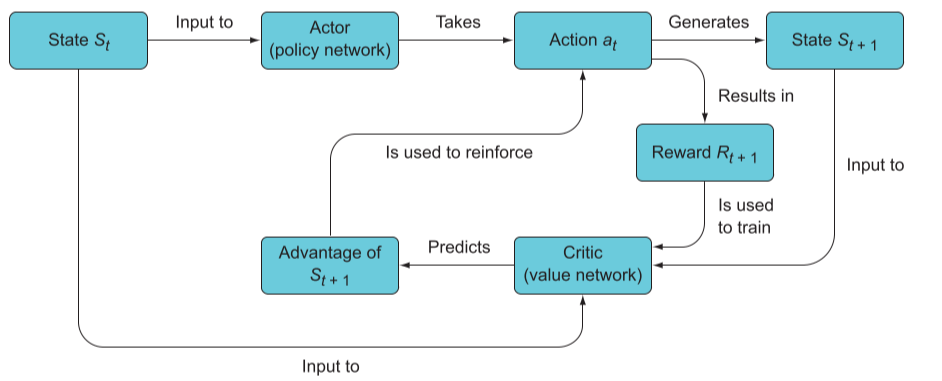
  • 首先，行动者预测最佳的动作，并产生新的状态
  • 批评者预测旧状态和新状态之间的优势，该优势用于训练行动者。
  • 行动者执行动作后的奖励来训练批评者

进化算法（Evolutionary algorithms）

以往我们通常依赖于神经网络来近似 Q 函数与策略函数，通过与环境交互、收集经验，然后使用反向传播来提高神经网络的准确性。但是该过程中，我们需要仔细地调整几个超参数，但不能保证模型的成功。而且要求损失函数具有可微性。

而进化算法用不同的参数衍生出多个智能体，观察哪一个做的最好，然后培育这个最好的，后代继承其特征继续训练。

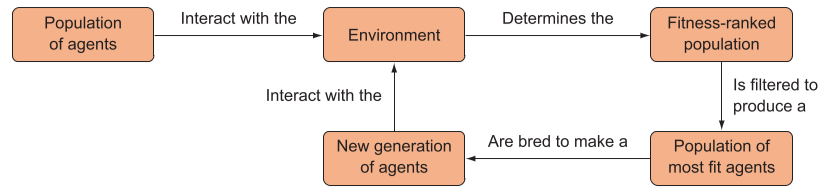
遗传算法流程

  • 生成随机参数向量的100个智能体
  • 在游戏中对模型迭代，记录奖励来评估个体的适合度
  • 按照相对适合度加权，从种群中随机抽取一对对个体，创建繁殖种群
  • 繁殖种群中的个体交配产生后代，形成相同规模的智能体
  • 交配过程可以是一对个体之间的参数进行简单的相互交换
  • 不断迭代种群，并加入一些随机突变，确保遗传多样性

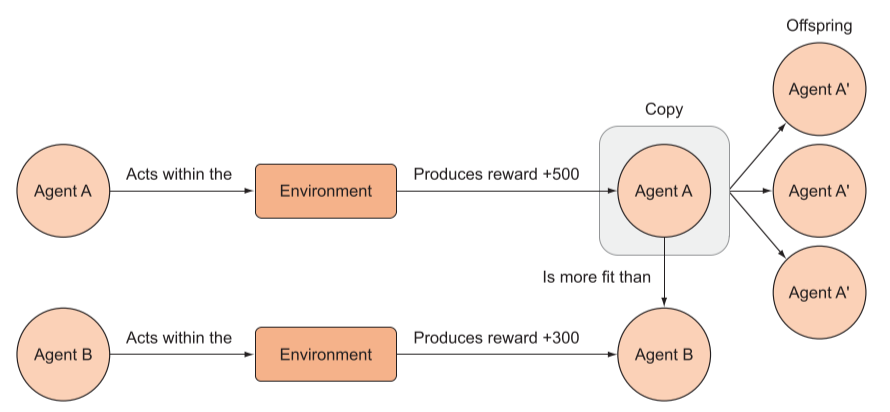
进化算法的优缺点

  • 往往比基于梯度的方法更具探索性
  • 遗传算法中的智能体不会推向任何方向。每一代中产生很多智能体，并且它们之间存在很多的随机变化，彼此具有不同的策略。
  • 需要大量的样本进行训练更新，效率远低于神经网络
0
机器学习

评论区