线代_行列式的几何意义

行列式（Determinant），记作det(A)或|A|，是一个在方阵(n*n)上计算得到的标量。行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。

书写法

矩阵A的行列式记作det(A)，行列式经常使用竖直线记法

$$\operatorname{det}(A)=|A|=\left|\begin{array}{lll} a & b & c \\ d & e & f \\ g & h & i \end{array}\right|$$

行列式在二维欧氏空间的几何意义

在一个二维平面上，两个向量和的行列式是

$$X=(a, c)$$

和

$$X^{\prime}=(b, d)$$

的行列式是：

$$\operatorname{det}\left(X, X^{\prime}\right)=\left|\begin{array}{ll} a & b \\ c & d \end{array}\right|=a d-b c$$

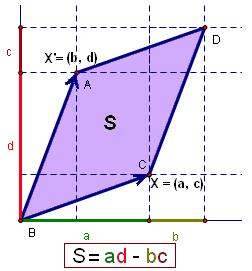
当系数是实数时，行列式表示的是向量X和X’形成的平行四边形的有向面积，并有如下性质：

• 行列式为零当且仅当两个向量共线（线性相关），这时平行四边形退化成一条直线
• 以逆时针方向为正向的话，将X逆时针“转到”X’处时，扫过的地方在平行四边形里为正，否则的话面积就是负的。
• 行列式是一个双线性映射，也就是将其中的一个向量分成两个并提取单位向量，最后的面积之和是一样的

$$\operatorname{det}\left(\lambda X+\mu Y, X^{\prime}\right)=\lambda \operatorname{det}\left(X, X^{\prime}\right)+\mu \operatorname{det}\left(Y, X^{\prime}\right)$$

行列式在三维欧氏空间的几何意义

在三维的有向空间中，三个三维向量的行列式是：

$$\operatorname{det}\left(X, X^{\prime}, X^{\prime \prime}\right)=\left|\begin{array}{ccc} x & x^{\prime} & x^{\prime \prime} \\ y & y^{\prime} & y^{\prime \prime} \\ z & z^{\prime} & z^{\prime \prime} \end{array}\right|=x y^{\prime} z^{\prime \prime}+x^{\prime} y^{\prime \prime} z+x^{\prime \prime} y z^{\prime}-x y^{\prime \prime} z^{\prime}-x^{\prime} y z^{\prime \prime}-x^{\prime \prime} y^{\prime} z$$

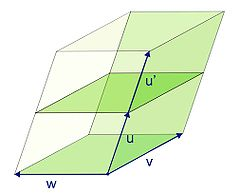
当系数是实数时，行列式表示X、X’和X’'三个向量形成的平行六面体的有向体积，性质如下：

• 行列式为零当且仅当三个向量共线或者共面（三者线性相关），这时平行六面体退化为平面图形，体积为零。
• 有向体积的定义，根据右手定则来约定。比如右图中$（u,v,w）$所形成的平行六面体的体积是正的，而 $（u,w,v）$所形成的平行六面体的体积是负的。
• 同样的也可以对几何体积和累加，其几何意义是指每组三个向量中如果有两个是重合的。

$$\operatorname{det}\left(a X+b Y, X^{\prime}, X^{\prime \prime}\right)=a \operatorname{det}\left(X, X^{\prime}, X^{\prime \prime}\right)+b \operatorname{det}\left(Y, X^{\prime}, X^{\prime \prime}\right)$$

参考：1、维基