矩阵内积(Inner product)与外积(Outer product)与迹(Trace)
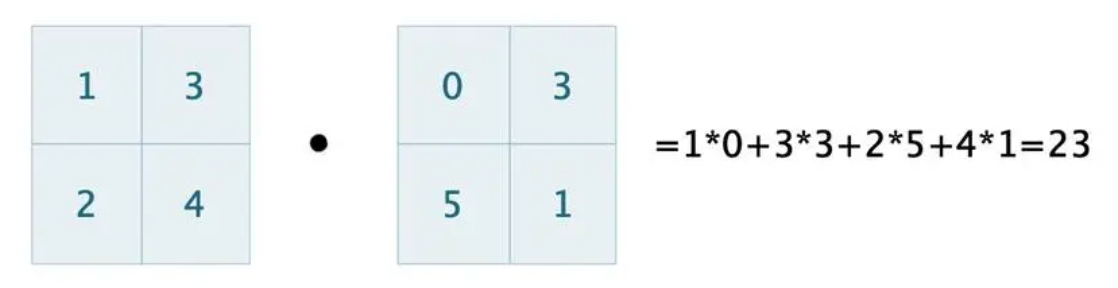
矩阵的内积 。具体地,对于两个m × n m×n m × n A , B A, B A , B 内积 定义为(对应相乘之和,结果为标量 ):
⟨ A , B ⟩ = ∑ i , j a i j b i j \langle A, B\rangle=\sum_{i, j} a_{i j} b_{i j}
⟨ A , B ⟩ = i , j ∑ a i j b i j
从定义可以看出 ⟨ A , B ⟩ = ⟨ B , A ⟩ \langle A, B\rangle=\langle B, A\rangle ⟨ A , B ⟩ = ⟨ B , A ⟩ 交换律 。对于方阵 A ∈ R m × m A \in \mathbb{R}^{m \times m} A ∈ R m × m A A A 迹 (对角线元素之和),记为Tr ( A ) = ∑ i = 1 m a i i \operatorname{Tr}(A)=\sum_{i=1}^m a_{i i} T r ( A ) = ∑ i = 1 m a i i Tr ( A ) = Tr ( A T ) \operatorname{Tr}(A)=\operatorname{Tr}\left(A^{\mathrm{T}}\right) T r ( A ) = T r ( A T )
矩阵的外积 。给定 m × 1 m \times 1 m × 1 u \mathbf{u} u 1 × n 1 \times n 1 × n v \mathbf{v} v u ⊗ v \mathbf{u} \otimes \mathbf{v} u ⊗ v m × n m \times n m × n A \mathbf{A} A
u ⊗ v = A = u v \mathbf{u} \otimes \mathbf{v}=\mathbf{A}=\mathbf{u} \mathbf{v}
u ⊗ v = A = u v
那么对于 m × n m \times n m × n A , B A, B A , B 内积 等于矩阵外积 的迹 :
⟨ A , B ⟩ = Tr ( A B T ) = Tr ( B T A ) . \langle A, B\rangle=\operatorname{Tr}\left(A B^{\mathrm{T}}\right)=\operatorname{Tr}\left(B^{\mathrm{T}} A\right) .
⟨ A , B ⟩ = T r ( A B T ) = T r ( B T A ) .
更一般地, 假设 A 1 , A 2 , ⋯ , A m A_1, A_2, \cdots, A_m A 1 , A 2 , ⋯ , A m 维数是相容 的 ( A i \left(A_i\right. ( A i A i + 1 , i = A_{i+1}, i= A i + 1 , i = 1 , 2 , ⋯ , m − 1 1,2, \cdots, m-1 1 , 2 , ⋯ , m − 1 A m A_m A m A 1 A_1 A 1
Tr ( A 1 A 2 ⋯ A m ) = Tr ( A 2 A 3 ⋯ A m A 1 ) = ⋯ = Tr ( A m A 1 ⋯ A m − 1 ) . \operatorname{Tr}\left(A_1 A_2 \cdots A_m\right)=\operatorname{Tr}\left(A_2 A_3 \cdots A_m A_1\right)=\cdots=\operatorname{Tr}\left(A_m A_1 \cdots A_{m-1}\right) .
T r ( A 1 A 2 ⋯ A m ) = T r ( A 2 A 3 ⋯ A m A 1 ) = ⋯ = T r ( A m A 1 ⋯ A m − 1 ) .
正交矩阵(Orthogonal matrix)
对于矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n 单位矩阵 I I I A T A = A A T = I A^{\mathrm{T}} A=A A^{\mathrm{T}}=I A T A = A A T = I A A A 正交矩阵 ,若其中 m > n m>n m > n 列正交矩阵 。其行向量 与列向量 皆为正交的单位向量 。
以下是一些重要的性质:
作为一个线性映射 (变换矩阵),正交矩阵保持距离不变,所以它是一个保距映射 ,具体例子为旋转矩阵 与镜射矩阵 。
行列式值为 +1 的正交矩阵,称为特殊正交矩阵 ,它是一个旋转矩阵 。行列式值为-1 的正交矩阵,称为瑕旋转矩阵 。瑕旋转是旋转加上镜射 。镜射也是一种瑕旋转。所有 n × n n \times n n × n O ( n ) O(n) O ( n ) 正交群 。亦即,正交矩阵与正交矩阵的乘积也是一个正交矩阵 。
所有特殊正交矩阵 对矩阵乘法形成一个子群 S O ( n ) S O(n) S O ( n ) 旋转矩阵与旋转矩阵的乘积也是一个旋转矩阵 。
正定矩阵(positive-definite matrix)与半正定矩阵(positive semi-definite matrix)
对于对称矩阵 A ∈ S m A \in \mathcal{S}^m A ∈ S m
f ( x ) = x T A x = ∑ i , j = 1 m a i j x i x j . f(x)=x^{\mathrm{T}} A x=\sum_{i, j=1}^m a_{i j} x_i x_j .
f ( x ) = x T A x = i , j = 1 ∑ m a i j x i x j .
如果对于任意的向量 x ∈ R m x \in \mathbb{R}^m x ∈ R m f ( x ) ⩾ 0 f(x) \geqslant 0 f ( x ) ⩾ 0 A A A 半正定矩阵 , 记 为 A ⪰ 0 A \succeq 0 A ⪰ 0
进一步地, 如果对于任意的非零向量 x x x f ( x ) > 0 f(x)>0 f ( x ) > 0 A A A 正定矩阵 , 记为 A ≻ 0 A \succ 0 A ≻ 0
根据正定矩阵和半正定矩阵的定义,半正定矩阵包括了正定矩阵。
正定矩阵使得向量M是沿着原向量 x x x 旋转角度小于90度 。
推荐两篇文章帮助理解:如何理解正定矩阵和半正定矩阵 浅谈「正定矩阵」和「半正定矩阵」
矩阵的秩(Rank)
给定一个 m × n m × n m × n A A A m m m 行向量的极大线性无关组 对应的向量个数称为矩阵的行秩 ;其 n n n 列向量的极大线性无关组 对应的向量个数称为矩阵的列秩 .矩阵的行秩等于列秩,称为矩阵的秩,且,秩=列秩=行秩 是恒成立的。记为:
rank ( A ) \operatorname{rank}(A)
r a n k ( A )
以下是一些重要的性质:
m × n m × n m × n m m m n n n 非负整数 ,表示为 rank ( A ) ≤ min ( m , n ) \operatorname{rank}(A) ≤ \operatorname{min}(m, n) r a n k ( A ) ≤ m i n ( m , n ) 有尽可能大的秩的矩阵被称为有满秩 ;类似的,否则矩阵是秩不足(或称为“欠秩 ”)。
只有零矩阵 有秩0
有了秩,讨论线性方程组 A x = b Ax = b A x = b 增广矩阵 A ^ = ( A , b ) \widehat{A}=(A, b) A = ( A , b ) 系数矩阵 的右边添上线性方程组等号右边的常数 列得到的矩阵。
如果方程组的解存在, 即 b b b A A A rank ( A ) = rank ( A ^ ) \operatorname{rank}(A)=\operatorname{rank}(\widehat{A}) r a n k ( A ) = r a n k ( A )
若 rank ( A ) < rank ( A ∣ B ) \operatorname{rank}(A)<\operatorname{rank}(A \mid B) r a n k ( A ) < r a n k ( A ∣ B )
若 rank ( A ) = rank ( A ∣ B ) = n \operatorname{rank}(A)=\operatorname{rank}(A \mid B)=n r a n k ( A ) = r a n k ( A ∣ B ) = n
若 rank ( A ) = rank ( A ∣ B ) < n \operatorname{rank}(A)=\operatorname{rank}(A \mid B)<n r a n k ( A ) = r a n k ( A ∣ B ) < n
rank ( A ) > rank ( A ∣ B ) \operatorname{rank}(A)>\operatorname{rank}(A \mid B) r a n k ( A ) > r a n k ( A ∣ B )
行空间与列空间
行空间定义(Row Space)
设一 m m m n n n A A A m × n m × n m × n 行空间 是由矩阵 A A A 所有行向量 所生成的 R n R^n R n 子空间 ,记作 C ( A T ) C(A^T) C ( A T ) R ( A ) R(A) R ( A ) A T A^T A T n × m n × m n × m
行空间 C ( A T ) C(A^T) C ( A T ) A A A 行向量的某种线性组合 ,都为 R n R^n R n n n n A A A min ( m , n ) \min(m,n) min ( m , n )
dim C ( A T ) = dim R ( A ) = rank ( A T ) ≤ min ( m , n ) \operatorname{dim}C(A^T)=\operatorname{dim}R({A})=\operatorname{rank}\left({A}^T\right) \leq \min \left(m, n\right)
d i m C ( A T ) = d i m R ( A ) = r a n k ( A T ) ≤ min ( m , n )
行空间 C ( A T ) C(A^T) C ( A T ) 自然基底 是矩阵 A A A 最大线性无关组 。
列空间定义 (Column Space)
设一 m m m n n n A ( m × n {A}\left(m \times n\right. A ( m × n R m {R}^m R m C ( A ) C({A}) C ( A ) A {A} A C ( A ) C({A}) C ( A ) A {A} A 列向量的某种线性组合 ,都为 R m {R}^m R m m m m C ( A ) C({A}) C ( A ) 维度等于矩阵 A {A} A ,最大为 min ( m , n ) \min (m, n) min ( m , n )
dim C ( A ) = rank ( A ) ≤ min ( m , n ) \operatorname{dim} C(\mathbf{A})=\operatorname{rank}(\mathbf{A}) \leq \min \left(m_{,} n\right)
d i m C ( A ) = r a n k ( A ) ≤ min ( m , n )
列空间 C ( A ) C(\mathbf{A}) C ( A ) A \mathbf{A} A 列向量的最大线性无关组 。
像空间和零空间
零空间(NULL Space)
矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n 零空间 是方程 A x = 0 Ax = 0 A x = 0 x x x A A A 核,核空间 。
N ( A ) = { x ∣ A x = 0 , x ∈ R n } \mathcal{N}(A)=\left\{x \mid A x=0, x \in \mathbb{R}^n\right\}
N ( A ) = { x ∣ A x = 0 , x ∈ R n }
由于零空间是解所构成的空间 ,因此从 x x x R n \mathbb{R}^{n} R n 子空间 ,取决于列向量的个数 。
对于任意矩阵A ,零向量 都是一个特解 ,因为A乘以零向量总是得到零向量,即A ⋅ 0 = 0 A·0=0 A ⋅ 0 = 0 至少包含零向量 。
如果A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n A A A 秩 为 r r r m m m 数量 。
如果 r < n r<n r < n A A A 线性相关 的向量,使得它们的线性组合等于零向量 。这意味着矩阵 A A A 非零向量 ,因为这些线性相关的向量可以表示为非零向量的线性组合。
如果 r = n r=n r = n A A A 零向量是唯一的特解 ,因此零空间只包含零向量。
像空间(Range Space)
** 像定义:在线性代数 中,像通常指一个线性变换 将一个向量空间映射到另一个向量空间的结果。例如,如果 A A A m × n m×n m × n n n n m m m A A A A x Ax A x 向量的集合 ,其中 x x x n n n
对于矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n
R ( A ) = { y ∣ y = A x , x ∈ R n } \mathcal{R}(A)=\left\{y \mid y=A x, x \in \mathbb{R}^n\right\}
R ( A ) = { y ∣ y = A x , x ∈ R n }
从定义容易看出, 像空间 R ( A ) \mathcal{R}(A) R ( A ) 维数 ,记为 dim ( R ( A ) ) \operatorname{dim}(\mathcal{R}(A)) d i m ( R ( A ) ) 秩 rank ( A ) \operatorname{rank}(A) r a n k ( A ) A x = b A x=b A x = b b ∈ R ( A ) b \in \mathcal{R}(A) b ∈ R ( A ) x ∗ + v x^*+v x ∗ + v A x ∗ = b , v ∈ N ( A ) A x^*=b, v \in \mathcal{N}(A) A x ∗ = b , v ∈ N ( A )
对于像空间与零空间的维数关系 ,不加证明地给出如下结论:
dim ( R ( A ) ) + dim ( N ( A ) ) = n \operatorname{dim}(\mathcal{R}(A))+\operatorname{dim}(\mathcal{N}(A))=n
d i m ( R ( A ) ) + d i m ( N ( A ) ) = n
进一步地, 给定任意矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n R n \mathbb{R}^n R n 交分解 :
R n = N ( A ) ⊕ R ( A T ) , x ⊥ y ∀ x ∈ N ( A ) , y ∈ R ( A T ) . \mathbb{R}^n=\mathcal{N}(A) \oplus \mathcal{R}\left(A^{\mathrm{T}}\right), \quad x \perp y \quad \forall x \in \mathcal{N}(A), y \in \mathcal{R}\left(A^{\mathrm{T}}\right) .
R n = N ( A ) ⊕ R ( A T ) , x ⊥ y ∀ x ∈ N ( A ) , y ∈ R ( A T ) .
这个结论在推导线性空间的一些基本性质时尤其有用.
参考文章:线性代数(2):列空间与零空间
行列式(Determinant)
定义方阵 的行列式 ,记为 det ( A ) \det(A) det ( A )
det ( A ) = ∑ σ ∈ S n ( − 1 ) τ ( σ ) ∏ i = 1 n a i σ ( i ) , \operatorname{det}(A)=\sum_{\sigma \in S_n}(-1)^{\tau(\sigma)} \prod_{i=1}^n a_{i \sigma(i)},
d e t ( A ) = σ ∈ S n ∑ ( − 1 ) τ ( σ ) i = 1 ∏ n a i σ ( i ) ,
其中 S n S_n S n 1 , 2 , ⋯ , n 1,2, \cdots, n 1 , 2 , ⋯ , n 全排列的集合 ,τ ( σ ) \tau(\sigma) τ ( σ ) σ \sigma σ 逆序数 .
对于两个方阵 A , B ∈ R n × n A, B \in \mathbb{R}^{n \times n} A , B ∈ R n × n c ∈ R c \in \mathbb{R} c ∈ R
det ( A ) = det ( A T ) \operatorname{det}(A)=\operatorname{det}\left(A^{\mathrm{T}}\right) d e t ( A ) = d e t ( A T ) det ( A B ) = det ( A ) det ( B ) \operatorname{det}(A B)=\operatorname{det}(A) \operatorname{det}(B) d e t ( A B ) = d e t ( A ) d e t ( B ) det ( c A ) = c n det ( A ) \operatorname{det}(c A)=c^n \operatorname{det}(A) d e t ( c A ) = c n d e t ( A )
根据行列式是否为 0 , 我们可以将方阵分为两类:奇异与非奇异 。对于方阵 A A A det ( A ) = 0 \operatorname{det}(A)=0 d e t ( A ) = 0 奇异的 ,否则为非奇异的 。
对于非奇异矩阵 A A A rank ( A ) = n \operatorname{rank}(A)=n r a n k ( A ) = n A A A rank ( A ) ⩽ n − 1 \operatorname{rank}(A) \leqslant n-1 r a n k ( A ) ⩽ n − 1 非奇异矩阵的满秩性 ,其对应的线性方程组的解总是存在并且唯一的 。
特征值(eigenvalue)与特征向量(eigenvector)
对于矩阵 A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n 非零向量 v ∈ R n v \in \mathbb{R}^n v ∈ R n λ ∈ R \lambda \in \mathbb{R} λ ∈ R A v = λ v A v=\lambda v A v = λ v λ \lambda λ 特征值 ,v v v A A A λ \lambda λ 特征向量 ,矩阵 A − λ I A-\lambda I A − λ I λ \lambda λ 特征子空间 。
即 v v v 线性变换 之后,得到的新向量仍然与原来的 v v v 同一条直线上 ,但其长度或方向也许会改变,λ \lambda λ 缩放的比例 。
如果特征值为正 ,则表示 v v v 方向不变 ;如果特征值为负 ,说明方向反转 ;如果特征值为0 ,则是表示缩回零点 。
A v = λ v A v=\lambda v
A v = λ v
I A v = I λ v , A v = ( λ I ) v , A v − ( λ I ) v = 0 IA v=I\lambda v, A v=(\lambda I)v,A v-(\lambda I)v=0
I A v = I λ v , A v = ( λ I ) v , A v − ( λ I ) v = 0
( A − λ I ) v = 0 (A-\lambda I)v=0
( A − λ I ) v = 0
以上的推导容易看出,根据线性方程组理论,为了使这个方程有非零解 ,矩阵 A − λ I A-\lambda I A − λ I 行列式 必须是零(参考零空间的推导),λ λ λ A A A 充要条件 是 det ( λ I − A ) = 0 \det(λI − A) = 0 det ( λ I − A ) = 0
由行列式的定义可知,det ( λ I − A ) \operatorname{det}(\lambda I-A) d e t ( λ I − A ) λ \lambda λ n n n A A A 特征多项式 , 一般用 p A ( λ ) p_A(\lambda) p A ( λ ) p A ( λ ) p_A(\lambda) p A ( λ ) n n n n n n 复根 。
特别地,对于一个对角矩阵 ,我们可知其特征值全体就是其对角线元素构成的集合 。对于特征值 λ \lambda λ 单特征值 ;如果它是特征多项式的重根,我们称之为重特征值 , n n n n n n
参考:特征值和特征向量wiki
逆矩阵(Inverse matrix)
给定一个 n n n 方阵 A A A n n n B B B A B = B A = I n AB = BA = I_n A B = B A = I n I n I_n I n n n n 单位阵 ,则称 A A A 可逆 的,且 B B B A A A 逆矩阵 ,记作 A − 1 A^{-1} A − 1
只有方阵 (n×n 的矩阵)才可能有逆矩阵 。若方阵 A A A A A A 非奇异方阵 或可逆方阵 。
在矩阵里是没有除 的概念的,但可以乘以逆矩阵 ,这和除 是相同的。
可逆矩阵在几何上有很重要的意义,它表示一个线性变换可以逆转回去 ,即存在一个逆变换,将变换后的结果映射回原来的向量。
其具有以下性质:
( A − 1 ) − 1 = A \left(A^{-1}\right)^{-1}=A ( A − 1 ) − 1 = A ( λ A ) − 1 = 1 λ × A − 1 (\lambda A)^{-1}=\frac{1}{\lambda} \times A^{-1} ( λ A ) − 1 = λ 1 × A − 1 ( A B ) − 1 = B − 1 A − 1 (A B)^{-1}=B^{-1} A^{-1} ( A B ) − 1 = B − 1 A − 1 ( A T ) − 1 = ( A − 1 ) T ( A T \left(A^{\mathrm{T}}\right)^{-1}=\left(A^{-1}\right)^{\mathrm{T}}\left(A^{\mathrm{T}}\right. ( A T ) − 1 = ( A − 1 ) T ( A T A \mathrm{A} A ) ) ) det ( A − 1 ) = 1 det ( A ) \operatorname{det}\left(A^{-1}\right)=\frac{1}{\operatorname{det}(A)} d e t ( A − 1 ) = d e t ( A ) 1
参考:数学乐-逆矩阵
但不是所有的矩阵都存在逆矩阵,若矩阵可以需要满足充要条件:det ( A ) \operatorname{det}\left(A\right) d e t ( A ) A A A A B = I n AB = I_n A B = I n
广义逆阵(Generalized inverse)
一般问题中,矩阵 A A A A ∈ R m × n A ∈ R^{m×n} A ∈ R m × n
A G A = A AGA = A
A G A = A
成立的 G ∈ R n × m G ∈ R^{n×m} G ∈ R n × m A A A 广义逆阵 。一般来说广义逆是不唯一的 .可以看到当 m = n m = n m = n A A A A − 1 A^{−1} A − 1
建构广义逆阵的目的是针对可逆矩阵以外的矩阵 (例如非方阵的矩阵)可以找到一矩阵有一些类似逆矩阵的特性 。任意的矩阵都存在广义逆阵 ,若一矩阵存在逆矩阵,逆矩阵即为其唯一的广义逆阵。
有些时候, 广义逆特指摩尔-彭若斯广义逆(Moore – Penrose) ,记为 A † A^\dagger A †
A A † A = A A A^{\dagger} A=A A A † A = A A † A A † = A † A^{\dagger} A A^{\dagger}=A^{\dagger} A † A A † = A † A A † A A^{\dagger} A A † A † A A^{\dagger} A A † A
可以证明这种广义逆矩阵总是存在且是唯一的。我们给出一种 Moore-Penrose 逆矩阵的构造方法,记 r = rank ( A ) r=\operatorname{rank}(A) r = r a n k ( A ) A A A 满秩分解 ,即 A = B C A=B C A = B C B ∈ R m × r , C ∈ R r × n B \in \mathbb{R}^{m \times r},C \in \mathbb{R}^{r \times n} B ∈ R m × r , C ∈ R r × n rank ( A ) = rank ( B ) = rank ( C ) = r \operatorname{rank}(A)=\operatorname{rank}(B)=\operatorname{rank}(C)=r r a n k ( A ) = r a n k ( B ) = r a n k ( C ) = r Moore - Penrose 逆矩阵 可以表示为
A † = C T ( C C T ) − 1 ( B T B ) − 1 B T . A^{\dagger}=C^{\mathrm{T}}\left(C C^{\mathrm{T}}\right)^{-1}\left(B^{\mathrm{T}} B\right)^{-1} B^{\mathrm{T}} .
A † = C T ( C C T ) − 1 ( B T B ) − 1 B T .
进一步地, 给出 Moore - Penrose 逆的一些性质。
( A † ) † = A \left(A^{\dagger}\right)^{\dagger}=A ( A † ) † = A ( A T ) † = ( A † ) T \left(A^{\mathrm{T}}\right)^{\dagger}=\left(A^{\dagger}\right)^{\mathrm{T}} ( A T ) † = ( A † ) T A † A A T = A T A^{\dagger} A A^{\mathrm{T}}=A^{\mathrm{T}} A † A A T = A T
有了 Moore - Penrose 广义逆矩阵之后, 对于线性方程组 A x = b A x=b A x = b b ∈ R ( A ) ) b \in \mathcal{R}(A)) b ∈ R ( A ) ) x = A † b + ( I − A † A ) w x=A^{\dagger} b+\left(I-A^{\dagger} A\right) w x = A † b + ( I − A † A ) w w ∈ R n w \in \mathbb{R}^n w ∈ R n
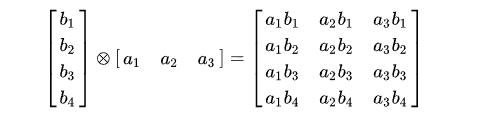




评论区