范数(Norm)

在数学上，范数包括向量范数和矩阵范数：

• 向量范数表征向量空间中向量的大小
• 矩阵范数表征矩阵引起变化的大小。

一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样。

对于矩阵范数，通过运算 $Ax=B$，可以将向量 $x$ 变化为 $B$，矩阵范数就是来度量这个变化大小的。

向量范数

称一个从向量空间 $\mathbb{R}^n$ 到实数域 $\mathbb{R}$ 的非负函数 $\|\cdot\|$ 为范数，它满足：

• 正定性: 对于所有的 $v \in \mathbb{R}^n$, 有 $\|v\| \geqslant 0$, 且 $\|v\|=0$ 当且仅当 $v=0$;
• 齐次性: 对于所有的 $v \in \mathbb{R}^n$ 和 $\alpha \in \mathbb{R}$, 有 $\|\alpha v\|=|\alpha|\|v\|$;
• 三角不等式: 对于所有的 $v, w \in \mathbb{R}^n$, 有 $\|v+w\| \leqslant\|v\|+\|w\|$.

L-P范数

与闵可夫斯基距离的定义一样，L-P范数不是一个范数，而是一组范数，其定义如下：

$$L_p=\|\mathbf{x}\|_p=\sqrt[p]{\sum_{i=1}^n x_i^p}, \mathbf{x}=\left(x_1, x_2, \ldots, x_n\right)$$

根据 $P$ 的变化，范数也有着不同的变化，一个经典的有关 $P$ 范数的变化图如下：

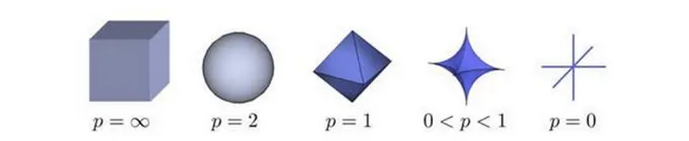
表示了 $P$ 从无穷到 0 变化时，三维空间中到原点的距离（范数）为 1 的点构成的图形的变化情况。以常见的 L-2 范数（$P=2$）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。

L0 范数

当 $P=0$ 时，也就是 L0 范数，L0 范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。根据 L-P 定义可以得到的 L0 的定义为：

$$\|\mathbf{x}\|_0=\sqrt[0]{\sum_{i=1}^n x_i^0}$$

非零元素的零次方为1，零的零次方和非零数开零次方不好定义，很不好说明 L0 的意义，所以在通常情况下，用的是：

$$\|\mathbf{x}\|_0=\#\left(i \mid x_i \neq 0\right)$$

表示向量 $x$ 中非零元素的个数。

其优化问题为：

$$\begin{aligned}&\begin{aligned}& \min \|\mathbf{x}\|_0 \\& \text { s.t. } A x=b\end{aligned}\end{aligned}$$

但由于L0范数本身不容易有一个好的数学表示形式，给出上面问题的形式化表示是一个很难的问题，故被人认为是一个 NP-hard 问题，即直接求解它很复杂、也不可能找到解。所以在实际情况中，L0 的最优问题会被转化到 L1 或 L2 下的最优化。

L1范数

当 $P=1$ 时，任意向量 $\mathbf{x}$ 的 L1范数为：

$$\|\mathbf{x}\|_1=\sum_{i=1}^n\left|x_i\right|$$

等于向量中所有元素绝对值之和。

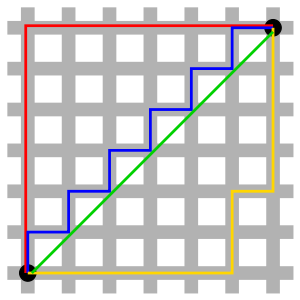
L1范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异，如曼哈顿距离（Manhattan distance）：例如在平面上，坐标（x1, y1）的点 P1 与坐标（x2, y2）的点 P2 的曼哈顿距离为：

$${\displaystyle d(x,y)=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|.}$$

曼哈顿与欧几里得距离： 红、蓝与黄线分别表示所有曼哈顿距离都拥有一样长度（12），而绿线表示欧几里得距离有6×√2 ≈ 8.48的长度。

对于L1范数，它的优化问题如下：

$$\begin{aligned}&\begin{aligned}& \min \|\mathbf{x}\|_1 \\& \text { s.t. } A x=b\end{aligned}\end{aligned}$$

机器学习中的 L1正则化

L1正则化是机器学习中的一种常用正则化方法，它可以帮助解决过拟合问题。L1正则化通过在目标函数中加入L1范数（绝对值和）惩罚项来约束模型的复杂度，使得模型更加简单和稀疏。

在线性回归等机器学习任务中，L1正则化的公式为：

$$J(w) = \frac{1}{2n} \sum_{i=1}^{n} (y_i - w^Tx_i)^2 + \lambda ||w||_1$$

其中，$J(w)$ 是目标函数，$w$ 是待求解的参数向量，$n$ 是样本数量，$x_i$ 是第 $i$ 个样本的特征向量，$y_i$ 是第 $i$ 个样本的标签，$\lambda$ 是正则化参数，$||w||_1$ 是 $w$ 的 L1 范数，即所有元素的绝对值之和。

通过最小化目标函数 $J(w)$，可以得到模型的最优参数 $w$，从而进行预测和分类等任务。

L1正则化在优化模型时会引入一个L1范数惩罚项，这个惩罚项是由参数向量中各个元素的绝对值之和组成的。这个惩罚项的作用是将参数向量中的一些元素“压缩”到0，从而达到降低模型复杂度、提高泛化能力的目的。

当正则化参数 $\lambda$ 越大时，L1范数惩罚项的作用就会越明显。在这种情况下，优化模型的目标函数不仅要最小化数据损失，还要尽可能地减小参数向量中的L1范数惩罚项。在模型训练过程中，这种约束会促使一些参数的取值逐渐趋近于0，而一些重要的参数则会被保留下来。这就是为什么L1正则化能够实现稀疏。

具体来说，L1正则化的效果与参数向量中各个元素的相关性有关。如果某些元素之间存在强相关性，那么这些元素的L1范数惩罚项就会相互抵消，这样模型就会将这些元素的权重分散到各个相关的元素中。但是，如果某个元素与其他元素之间的相关性较小，那么它的L1范数惩罚项就会独立地影响它的权重。这就会促使模型将其权重设置为0，从而实现稀疏性。

因此，L1正则化的稀疏性可以帮助模型减少不必要的特征或参数，提高模型的泛化能力和效率。

L2范数

L2范数是最常见的范数，欧氏距离就是一种L2范数，它的定义如下：

$$\|\mathbf{x}\|_2=\sqrt{\sum_{i=1}^n x_i^2}$$

表示向量元素的平方和再开平方。

像L1范数一样， L2也可以度量两个向量间的差异，如平方差和 (Sum of Squared Difference)：

$$S S D\left(x_1, x_2\right)=\sum_{i=1}^n\left(x_{1 i}-x_{2 i}\right)^2$$

对于L2范数，它的优化问题如下:

$$\begin{aligned}& \min \|x\|_2 \\& \text { s.t. } A x=b\end{aligned}$$

L2范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

机器学习中的 L2正则化

L2正则化在优化模型时会引入一个L2范数惩罚项，这个惩罚项是由参数向量中各个元素的平方和组成的。这个惩罚项的作用是限制参数向量中各个元素的大小，从而达到降低模型复杂度、提高泛化能力的目的。

L2正则化的公式如下：

$$L_{2}(\theta)=\frac{\lambda}{2}\sum_{i=1}^{n}\theta_{i}^{2}$$

其中，$\theta$ 是模型的参数向量，$n$ 是参数向量中元素的数量，$\lambda$ 是正则化强度的超参数，控制正则化项在总损失函数中的权重。

在模型训练过程中，L2正则化会限制参数向量中各个元素的大小，避免过大或过小的参数出现，从而防止模型在训练集上出现过拟合的问题。此外，L2正则化还能够促使参数向量中的元素趋向于分布在均值附近，这有助于降低模型的方差，提高泛化能力。

需要注意的是，L2正则化对于大多数参数都会施加惩罚项，但并不会将任何参数设为0。与L1正则化不同，L2正则化不会实现稀疏性。

$L_{\infty}$ 范数

当 $P =\infty$时，也称为最大值范数（maximum norm），是向量中所有元素绝对值的最大值，它是 L-P 范数的一种特殊情况，其中p的值趋近于无穷大，$L_{\infty}$ 范数定义为

$$\|\mathbf{x}\|_{\infty}=\max \left(\left|x_i\right|\right)$$

常常用于限制模型的权重或梯度的最大值，从而防止模型的过拟合或梯度爆炸的问题。在优化算法中，$L_{\infty}$范数正则化可以通过对权重或梯度进行截断，使其不超过某个阈值，从而控制它们的大小。

矩阵范数

矩阵范数是一种将矩阵映射为标量的函数，它度量矩阵的大小、形状和特征，类似于向量的范数。常见的矩阵范数有以下几种：

L1范数：矩阵中每一列元素绝对值之和的最大值。矩阵L1范数的值越小，说明矩阵的稀疏性越高。

$$\|A\|_{1}=\max _{j} \sum_{i=1}^{m}\left|a_{i j}\right|$$

L2范数：矩阵的奇异值分解（Singular Value Decomposition，SVD）中，矩阵对角线上奇异值的平方和再开平方根。其中，$\lambda_{\max}$ 表示矩阵$A^{T}A$的最大特征值。可以衡量矩阵在向量空间中的长度和变换后的保持性质。

$$\|A\|_{2}=\sqrt{\lambda_{\max }\left(A^{T} A\right)}$$

无穷范数：矩阵中每一行元素绝对值之和的最大值。

$$\|A\|_{\infty}=\max _{i} \sum_{j=1}^{n}\left|a_{i j}\right|$$

Frobenius范数：矩阵中所有元素的平方和再开平方根。可以衡量矩阵与零矩阵之间的距离，同时也可以用于度量矩阵的复杂度和稳定性。

$$\|A\|_{F}=\sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n}\left|a_{i j}\right|^{2}}$$

核范数（nuclear norm）也称为矩阵的Schatten-$p$范数，是指矩阵的奇异值之和。对于矩阵 $A \in \mathbb{R}^{m\times n}$，它的核范数表示为 $|A|_{*}$，可以使用奇异值分解（Singular Value Decomposition，SVD）求解：

$$\|A\|_*=\sum_{i=1}^r \sigma_i,$$

其中 $\sigma_i, i=1,2, \cdots, r$ 为 $A$ 的所有非零奇异值, $r=\operatorname{rank}(A)$. 类似于向量的 $\ell_1$ 范数的保稀疏性, 我们也经常通过限制矩阵的核范数来保证矩阵的低秩性。

矩阵内积

对于矩阵空间 $\mathbb{R}^{m \times n}$ 的两个矩阵 $A$ 和 $B$, 除了定义它们各自的范数以外，我们还可以定义它们之间的内积，范数一般用来衡量矩阵的模的大小，而内积一般用来表征两个矩阵（或其张成的空间）之间的夹角。常用的内积-Frobenius 内积。$m \times n$ 矩阵 $A$ 和 $B$ 的 Frobenius 内积定义为

$$\langle A, B\rangle \stackrel{\text { def }}{=} \operatorname{Tr}\left(AB^{\mathrm{T}}\right)=\sum_{i=1}^m \sum_{j=1}^n a_{i j} b_{i j}$$

易知其为两个矩阵逐分量相乘的和，因而满足内积的定义。

导数

凸集与凸函数