三维形状表示方法：显式与隐式

显式表示方法

显式表示方法直接存储三维形状的表面信息，通常通过顶点、边和面的集合来描述。以下是一些常见的显式表示方法：

1. 多边形网格（Polygon Mesh）：

   • 描述：通过顶点、边和面来表示形状的表面，最常见的是三角网格。
   • 优点：直观且易于渲染，广泛应用于计算机图形学。
   • 应用：三维建模、动画、游戏、虚拟现实。

2. 点云（Point Cloud）：

   • 描述：通过一组三维坐标点来表示形状的表面。
   • 优点：简单且直接，可以从激光扫描或深度相机中获取。
   • 应用：三维扫描、环境感知、SLAM（同时定位与地图构建）。

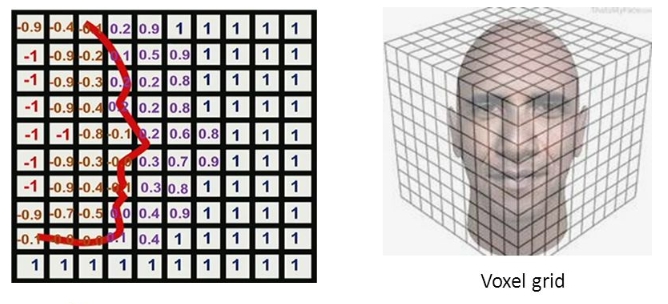
3. 体素网格（Voxel Grid）：

   • 描述：通过三维空间中的离散体素来表示形状，类似于三维像素。
   • 优点：适合表示体积数据，易于进行布尔运算和体积测量。
   • 应用：医学成像（如CT、MRI）、物理模拟。

4. 边界表示（Boundary Representation, B-Rep）：

   • 描述：通过边界曲面和边界线来表示形状。
   • 优点：精确表示复杂几何形状，常用于CAD（计算机辅助设计）。
   • 应用：机械设计、建筑设计。

5. 参数化曲面（Parametric Surface）：

   • 描述：通过参数方程来表示曲面，如Bezier曲面、NURBS（非均匀有理B样条）等。
   • 优点：能够精确控制曲面的形状和光滑度。
   • 应用：工业设计、汽车制造、动画制作。

隐式表示方法

隐式表示方法使用数学函数或神经网络来间接描述三维形状，而不是直接存储形状的表面信息。以下是一些常见的隐式表示方法：

1. 带符号距离函数（Signed Distance Function, SDF）：

   • 描述：SDF通过一个标量场来表示，每个点的值是其到最近表面的距离，带符号表示在表面内外。
   • 优点：能够平滑地表示复杂的几何形状，适合处理拓扑变化。
   • 应用：三维重建、碰撞检测、流体模拟。

2. 截断带符号距离函数（Truncated Signed Distance Function, TSDF）：

   • 描述：TSDF是SDF的一种变体，通过截断距离值来减少计算复杂度和存储需求。
   • 优点：适合用于实时三维重建和融合多视角数据。
   • 应用：实时三维重建（如KinectFusion）。

3. 神经隐式表示（Neural Implicit Representation）：

   • 描述：使用神经网络（如多层感知器，MLP）来学习和表示三维形状，输入为坐标点，输出为该点的属性（如SDF值、密度值等）。
   • 优点：能够表示非常复杂的几何结构，并且具有良好的泛化能力。
   • 应用：DeepSDF、NeRF（Neural Radiance Fields）等。

4. 二元空间分割树（Binary Space Partitioning, BSP）：

   • 描述：通过递归地将空间划分为两部分来表示形状。
   • 优点：适合表示布尔运算的结果，如并集、交集、差集。
   • 应用：计算机图形学中的布尔操作。

带符号距离函数（Signed Distance Function, SDF）

带符号距离函数（Signed Distance Function, SDF）是一种用于表示三维几何形状的方法，通过定义三维空间中每个点到最近表面的距离来描述物体的形状。SDF的值带有符号，以表示点在物体表面内外的位置。以下是对SDF的详细介绍：

SDF的定义和基本概念

1. 距离函数：

   • SDF定义了空间中每个点 ( p ) 到物体表面最近点的距离$d(p)$。
   • 符号 ( s ) 表示距离的正负号：
     • $s > 0$ 表示点在表面外部。
     • $s < 0$ 表示点在表面内部。
     • $s = 0$ 表示点在表面上。

2. 数学表示：

   • 对于给定点$p$，SDF函数 $\phi(p)$表示为：

$$\phi(p) = \begin{cases} -\text{dist}(p, \partial \Omega) & \text{if } p \in \Omega \\ +\text{dist}(p, \partial \Omega) & \text{if } p \notin \Omega \end{cases}$$

其中 $\Omega$ 是物体的内部，$\partial \Omega$ 是物体的表面，$\text{dist}(p, \partial \Omega)$ 是点 $p$ 到最近表面的距离。

SDF的计算和表示

1. 体素网格表示：

   • 空间被离散化为一个三维体素网格，每个体素存储一个SDF值。
   • 这种方法易于实现和计算，但需要较大的存储空间。

2. 连续函数表示：

   • 使用数学函数（如多项式、分段函数）或神经网络来表示SDF。
   • 这种方法可以减少存储需求，并且在某些情况下可以提供更高的精度。

截断带符号距离函数（Truncated Signed Distance Function, TSDF）

截断带符号距离函数（Truncated Signed Distance Function, TSDF）是一种用于三维重建和表示的方法，通过存储每个体素（voxel）到最近表面的距离及其符号，来描述三维空间中的物体表面。TSDF在计算带符号距离函数（Signed Distance Function, SDF）的基础上引入了截断距离的概念，以提高计算效率和减少存储需求。以下是对TSDF的详细介绍：

1. TSDF的基本概念

定义：

• TSDF通过存储每个体素到最近表面的带符号距离来描述三维形状。
• 距离值带有符号，正值表示点在表面外部，负值表示点在表面内部，零值表示点在表面上。

截断距离：

• 为了减少计算复杂度和存储需求，TSDF对距离值进行截断。
• 设定一个最大截断距离值 $\mu$，所有大于 $\mu$ 或小于$-\mu$ 的距离值将被截断为$\mu$ 或$-\mu$。

2. TSDF的计算方法

初始化体素网格：

• 创建一个三维体素网格，每个体素存储一个TSDF值，初始值通常设为正的截断距离 $\mu$。

深度图更新：

• 使用多个视角的深度图来更新体素网格中的TSDF值。每个深度图提供了一视角下的物体表面距离信息。

距离计算和截断：

• 对于深度图中的每个像素，通过射线投影找到对应的体素，并计算该体素中心到表面的距离。
• 根据距离值和符号更新体素的TSDF值：

$$\phi(p) = \begin{cases} \mu & \text{if } d(p) > \mu \\ -\mu & \text{if } d(p) < -\mu \\ d(p) & \text{if } -\mu \leq d(p) \leq \mu \end{cases}$$

其中，$d(p)$ 是点 $p$ 到最近表面的实际距离。

神经隐式表示（Neural Implicit Representation）

神经隐式表示（Neural Implicit Representation）是一种使用神经网络来表示和生成三维几何形状的方法。与传统的显式表示方法（如多边形网格、体素网格）不同，神经隐式表示使用神经网络的连续函数来隐式地描述形状。这种方法近年来在计算机图形学和计算机视觉领域取得了显著的进展。以下是对神经隐式表示的详细介绍：

基本概念

神经隐式表示的核心思想是使用神经网络来学习一个隐式函数，该函数能够为给定的三维空间点提供该点的某种属性，例如带符号距离函数（SDF）值、密度值或颜色值。

1. 输入：

   • 三维坐标点 ((x, y, z))

2. 输出：

   • SDF值：该点到最近表面的带符号距离。
   • 密度值：该点的密度或物体存在的概率（用于体积渲染）。
   • 颜色值：该点的颜色信息（用于光线追踪和渲染）。

神经隐式表示的类型

1. 带符号距离函数（SDF）表示：
   • 使用神经网络学习SDF，输入为三维坐标点，输出为该点的SDF值。
   • 适用于精确表示物体的几何形状。

2. 体素表示（Volumetric Representation）：

   • 使用神经网络学习体素密度，输入为三维坐标点，输出为该点的密度值。
   • 适用于体积渲染和物体存在概率表示。

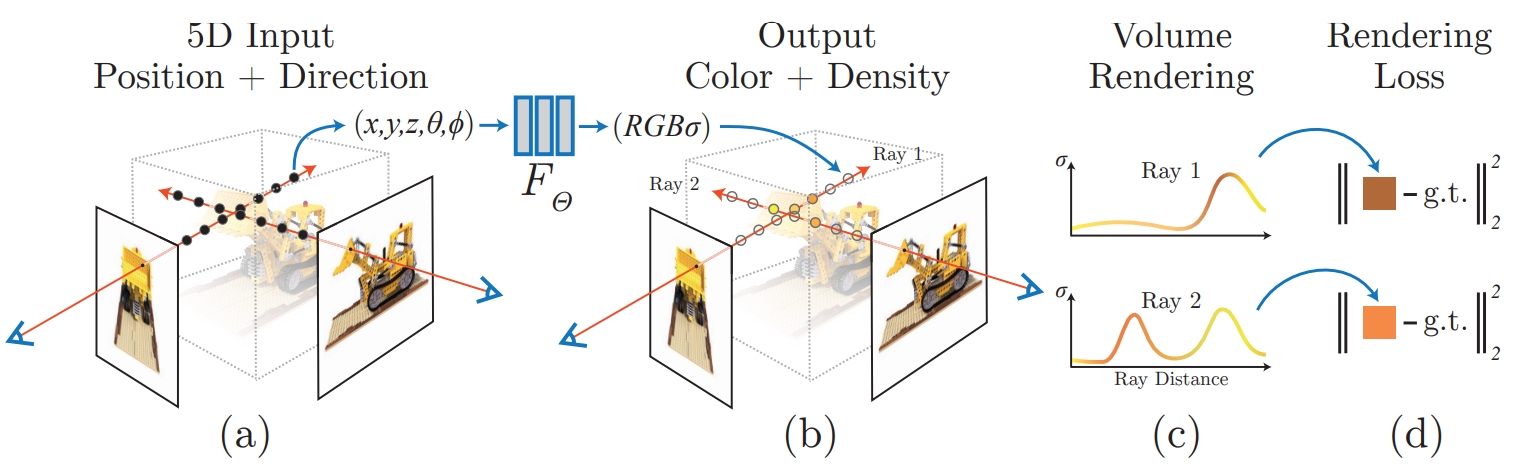
3. 辐射场表示（Neural Radiance Fields, NeRF）：

   • 使用神经网络学习三维空间中的颜色和密度分布，输入为三维坐标点和视角方向，输出为该点的颜色和密度。
   • 适用于真实感渲染和光线追踪。

实现方法

1. 神经网络架构：

   • 常用的网络架构是多层感知器（MLP），具有输入层、多个隐藏层和输出层。
   • 输入层接收三维坐标点，隐藏层通过非线性激活函数处理数据，输出层生成目标属性值。

2. 训练数据：

   • 采集用于训练的三维点和对应的目标值（如SDF值、密度值或颜色值）。
   • 数据来源可以是实际扫描的点云、深度图、图像等。

3. 损失函数：

   • 根据具体任务设计损失函数，用于衡量网络输出与真实值之间的差异。
   • 常用的损失函数包括均方误差（MSE）、交叉熵损失等。

4. 训练过程：

   • 使用梯度下降等优化算法，最小化损失函数，调整神经网络的参数。
   • 迭代训练直至网络收敛，能够准确预测三维点的属性值。

优点

1. 连续表示：

   • 神经隐式表示提供了一种连续的形状表示方法，能够精确描述复杂的几何形状。
   • 不依赖于离散网格，避免了分辨率限制问题。

2. 高效存储：

   • 通过神经网络参数表示形状，存储需求远小于传统的显式表示方法（如网格或体素）。

3. 良好的泛化能力：

   • 神经网络具有良好的泛化能力，能够在训练数据之外的区域生成合理的形状。

挑战和局限

1. 训练时间：

   • 训练神经网络可能需要大量的计算资源和时间，尤其是处理复杂的三维数据时。

2. 依赖数据质量：

   • 神经隐式表示的效果高度依赖于训练数据的质量和覆盖范围。

3. 实时性：

   • 实时应用中的推理速度可能受到网络复杂性的限制，需要优化和加速技术。

Ref：
3D 形状和场景的神经隐式表示