对于刚体而言，它们的所有组件(零件、点、面或任何东西)都在一个自身的局部参考系中刚性地指定(它们在这个参考系中构成常数参数，即位置相对固定)。因此，刚性物体的运动可以完全由自身参照系的运动来表示。（参考系与坐标系的区别）

参考系定义

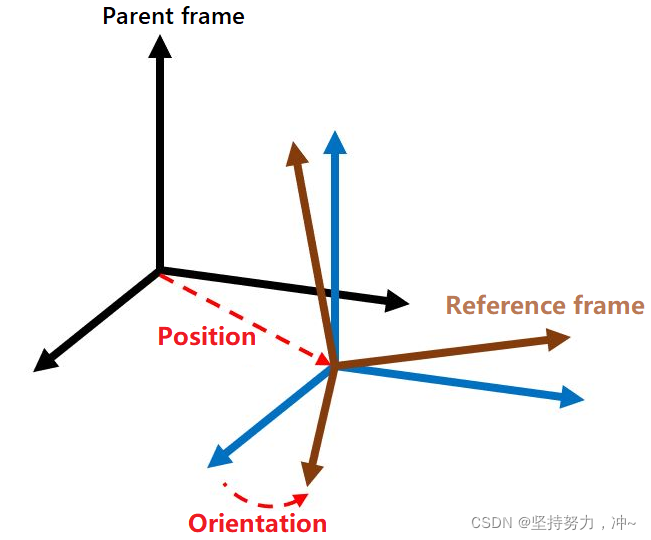
相对参考系（Reference frame）由其处于另一参考系的坐标系（Coordinate）原点的位置（Position）和方向（Orientation）定义，并将该参考系称为父参考系（Parent frame）。

我们将所有参考系的父参考系称为全局参考系，全局参考系通常被认为是静态的，通常在SLAM中第一帧的会被默认为全局参考系。
我们将位置（Position）和方向（Orientation）合并定义为位姿（Pose）。
以下是对上述关系的数学符号定义约定：

刚体B上的点或向量要用上标或下标加以指示： $\mathbf{p} _{B},\mathbf{v} _{B},\mathbf{p}^{B},\mathbf{v}^{B}$
而在全局参考系上的点或向量可以无需上下标： $\mathbf{p},\mathbf{v}$
刚体B相对于参考系F的位姿为： $\mathit{B} _{\mathit{F} }$ ，也可以表述为： $\mathit{B} _{\mathit{F} }=(\mathbf{t_{\mathit{FB} } },\mathbf{\Phi}_{\mathit{FB} })$ 。其中 $\mathbf{t_{\mathit{FB} } }$ 是一个平移向量表示刚体B在坐标系F中的位置， $\mathbf{\Phi}_{\mathit{FB} }$ 则是刚体B相对于参考系F的旋转量。

在2D中，平移向量为 $\mathbf{t} =(a,b)$ ,而旋转量 $\mathbf{\Phi}$ 定义为θ，

B=\left[\begin{array}{l} \mathbf{t} \\ \theta \end{array}\right] \in \mathbb{R}^{3}

在2D中，平移向量为 $\mathbf{t} =(a,b,c)$ ,而旋转量 $\mathbf{\Phi}$ 则有许多种形式，例如欧拉角、四元数、旋转矩阵。为了表述的完整与方便这里统一采用四元数， $\mathbf{q} =[qw, qx, qy, qz] ^{T}$

B=\left[\begin{array}{l} \mathbf{t} \\ \mathbf{q} \end{array}\right] \in \mathbb{R}^{7}, \quad\|\mathbf{q}\|=1

坐标变换

一个刚体参照系中的点或向量是可以通过坐标变换运算在另一个坐标系中表达的。例如，在某个刚体B中相对与全局参考系为： $\mathit{B}=(\mathbf{t},\mathbf{\Phi})$ ，而其上的一个点或向量则表述为：

\begin{array}{l} \mathbf{p}=\mathbf{R}\{\boldsymbol{\Phi}\} \mathbf{p}_{B}+\mathbf{t} \\ \mathbf{v}=\mathbf{R}\{\boldsymbol{\Phi}\} \mathbf{v}_{B} \end{array}

反推关系为：

\begin{array}{l} \mathbf{p}_{B}=\mathbf{R}\{\boldsymbol{\Phi}\}^{\top}(\mathbf{p}-\mathbf{t}) \\ \mathbf{p}_{B}=\mathbf{R}\{\boldsymbol{\Phi}\}^{\top} \mathbf{p} \end{array}

注意点：这里， $\mathbf{R}\left\{\mathbf{\Phi}\right\}$ 是与方向 $\mathbf{\Phi}$ 有关的旋转矩阵。它的表达式取决于空间维度(2D或3D)表达方式。

在二维世界中， $\mathbf{R}\left\{θ\right\}$ 是与旋转角θ相关的旋转矩阵：

\mathbf{R}\{\theta\}=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]

在三维世界中， $\mathbf{R}\left\{q\right\}$ 是与四元数q相关的旋转矩阵：

\mathbf{R}\{\mathbf{q}\}=\left[\begin{array}{ccc} q_{w}^{2}+q_{x}^{2}-q_{y}^{2}-q_{z}^{2} & 2\left(q_{x} q_{y}-q_{w} q_{z}\right) & 2\left(q_{x} q_{z}+q_{w} q_{y}\right) \\ 2\left(q_{x} q_{y}+q_{w} q_{z}\right) & q_{w}^{2}-q_{x}^{2}+q_{y}^{2}-q_{z}^{2} & 2\left(q_{y} q_{z}-q_{w} q_{x}\right) \\ 2\left(q_{x} q_{z}-q_{w} q_{y}\right) & 2\left(q_{y} q_{z}+q_{w} q_{x}\right) & q_{w}^{2}-q_{x}^{2}-q_{y}^{2}+q_{z}^{2} \end{array}\right]

首先我们假设一个移动机器人的相对参考系为R，并安装了一个相机，其相对坐标系为S，相机相对于移动机器人的相对参考系为： $S_{\mathit{R} }$ 。
类似于向量的相加，我们定义 $\oplus$ 为参考系相加。例如，我们将R和 $S_{\mathit{R} }$ 相加得到S：

而将 $\ominus$ 定义为参考系相减。例如，我们将S和R相减得到 $S_{\mathit{R} }$ ：

其中S、R和 $S_{\mathit{R} }$ 已知：

则根据以上的公式，在已知其中两个的情况下可以推导出另一个。

\begin{aligned} S &=\left[\begin{array}{l} \mathbf{t}_{S} \\ \theta_{S} \end{array}\right]=\left[\begin{array}{c} \mathbf{t}_{R}+\mathbf{R}\left\{\theta_{R}\right\} \mathbf{t}_{R S} \\ \theta_{R}+\theta_{R S} \end{array}\right] \\ S_{R} &=\left[\begin{array}{l} \mathbf{t}_{R S} \\ \theta_{R S} \end{array}\right]=\left[\begin{array}{c} \mathbf{R}\left\{\theta_{R}\right\}^{\top}\left(\mathbf{t}_{S}-\mathbf{t}_{R}\right) \\ \theta_{S}-\theta_{R} \end{array}\right] \end{aligned}

注意点：S是相对全局参考系，因此 $\mathbf{t} _{RS}$ （S相对R的位置）需要先乘以 $\mathbf{R}\left\{θ_{R}\right\}$ 转换到全局参考系。这里请参照上图仔细想，谁相对于谁旋转！！！

\begin{aligned} S &=\left[\begin{array}{c} \mathbf{t}_{S} \\ \mathbf{q}_{S} \end{array}\right]=\left[\begin{array}{c} \mathbf{t}_{R}+\mathbf{R}\left\{\mathbf{q}_{R}\right\} \mathbf{t}_{R S} \\ \mathbf{q}_{R} \otimes \mathbf{q}_{R S} \end{array}\right] \\ S_{R} &=\left[\begin{array}{c} \mathbf{t}_{R S} \\ \mathbf{q}_{R S} \end{array}\right]=\left[\begin{array}{r} \mathbf{R}\left\{\mathbf{q}_{R}\right\}^{\top}\left(\mathbf{t}_{S}-\mathbf{t}_{R}\right) \\ \mathbf{q}_{R}^{*} \mathbf{q}_{S} \end{array}\right] \end{aligned}