定义

点云配准是指将多个点云数据集在相同坐标系下进行对齐的过程，使得它们在空间中具有一致的位置和姿态。在点云配准中，需要估计点云之间的转换关系，包括平移、旋转和尺度（非刚性配准）等变换。

点云配准可以分为粗配准（Coarse Registration）和精配准（Fine Registration）两步。粗配准指的是在两幅点云之间的变换完全未知的情况下进行较为粗糙的配准，目的主要是为精配准提供较好的变换初值；精配准则是给定一个初始变换，进一步优化得到更精确的变换。

ICP 方法

点云 ICP 算法是一种经典的点云配准算法，其全称为Iterative Closest Point算法，是一种迭代优化的方法，用于将两个或多个点云数据集对齐。该算法通过迭代找到最优的刚体变换矩阵，使得两个点云之间的重叠部分最大化，从而实现点云的配准。由PJ Besl ，ND Mckay 在1992年提出的一种基于自由形态曲面的配准方法（原文）。

将该问题数理的描述为：假设存在两个空间点云集 $P、Q$ ，通过对 $Q$ 进行 $Rt$ 刚性变换，使得 $P、Q$ 点云集之间的差异最小。

R^{*}, t^{*}={\arg \min } \frac{1}{\left|Q_{s}\right|} \sum_{i=1}^{\left|Q_{s}\right|}\left\|p^{i}-\left(R \cdot q^{i}+t\right)\right\|^{2}

基本的算法步骤如下：

对点云进行预处理，例如滤波，降采样等
计算点集 $Q_i$ 中的若干点在点集 $P$ 中的最近点
求上述对应最近点对平均距离最小的旋转变化矩阵 $Rt_i$
对点集 $Qi$ 使用上述求的 $Rt_i$ 进行变换得到点集 $Q_{i+1}$
若点集 $P$ 与点集 $Qi+1$ 的某些损失函数小于一定阈值（例如最近点的平均距离），则可以停止迭代，否则回到第二步骤继续。

进一步拆分问题为：寻找点云集中的最近点、计算最优变换矩阵 $RT$

最优变换矩阵 (SVDICP)

具体的推导参考文献：链接、以及解读文章

总体计算最优平移 $t$ 和旋转 $R$ 的步骤：

计算两个点集的加权质心

\overline{\mathbf{p}}=\frac{\sum_{i=1}^{n} w_{i} \mathbf{p}_{i}}{\sum_{i=1}^{n} w_{i}}, \quad \overline{\mathbf{q}}=\frac{\sum_{i=1}^{n} w_{i} \mathbf{q}_{i}}{\sum_{i=1}^{n} w_{i}}

将两个点云同时平移到质心坐标系

\mathbf{x}_{i}:=\mathbf{p}_{i}-\overline{\mathbf{p}}, \quad \mathbf{y}_{i}:=\mathbf{q}_{i}-\overline{\mathbf{q}}, \quad i=1,2, \ldots, n

计算协方差矩阵 $S$ ，其中 $X$ ， $Y$ 是 $d \times n$ 大小的矩阵，即对应的 $\mathbf{x}_{i}$ 和 $\mathbf{y}_{i}$ 点云的坐标值。 $W$ 是权重对角矩阵。

S=XWY^\mathbf{T}

对 $S=U\sum V^\mathbf{T}$ 求 SVD 分解，根据公式求得 $R$

R=V\left(\begin{array}{ccccc}1 & & & & \\& 1 & & & \\& & \ddots & & \\& & & 1 & \\ & & & \operatorname{det}\left(V U^{\top}\right)\end{array}\right) U^{\top}

最后，根据公式计算 $t$

\mathbf{t}=\overline{\mathbf{q}}-R\overline{\mathbf{p}} \quad

迭代

常用的 ICP 算法停止迭代的条件有以下几种：

最大迭代次数：设定一个最大的迭代次数，当达到该次数后，算法强制停止迭代。
损失函数误差：设定一个损失误差阈值，迭代的误差小于该阈值时，算法停止迭代。
迭代损失误差变化率：如果当前迭代与上一次迭代的误差变化率小于设定的阈值，算法停止迭代。

根据不同应用场景和需求，选择适合的停止条件可以提高算法的效率和精度。

优缺点

ICP 算法的优点：其简单易懂，不用复杂的预处理，初值较好情况下，精度和收敛性都不错。

ICP 算法的缺点，在以下几个方面：

对于初值的敏感度较高，如果初值选的不好，则有可能会陷入局部最优解。
ICP算法只能对刚性变换进行配准，对于非刚性变换无法适用。
ICP算法的时间复杂度较高，对于大规模的点云配准需要消耗大量的计算资源和时间。

改进型算法

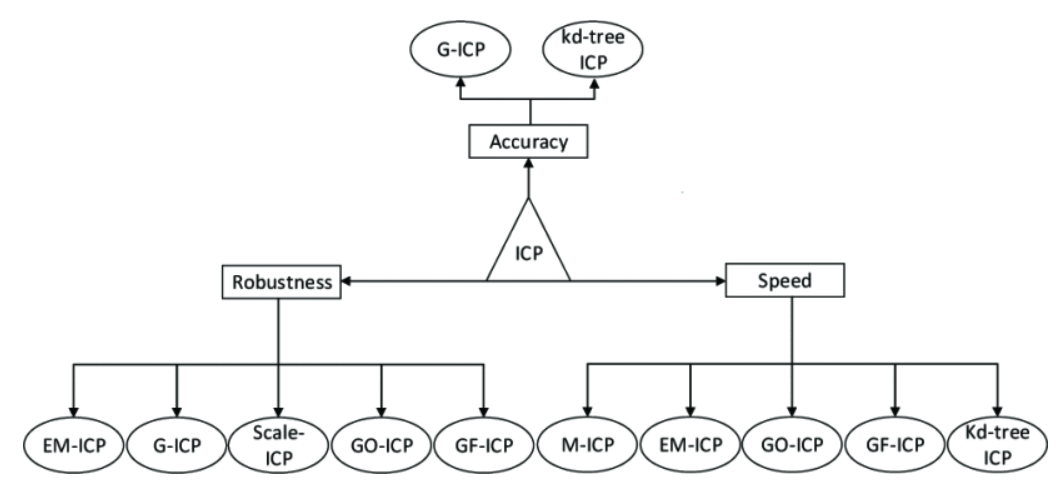
针对 ICP 所存在的问题，近些年有不同提升算法提出，总的可以分为三个方向：精度、鲁棒性、速度。

M-ICP (2002)

Multiresolution - ICP (M - ICP) 由Timothee Jost 提出了一种由粗到细的多分辨率方法来加速ICP算法，降低最近点搜索的复杂度。其算法原理是：使用少量采样数据（保持数据集点超过最小值）进行前几次迭代计算，并连续提高迭代分辨率，从而达到提高搜索速度的目标。

首先提出了三种不同分布下的迭代增益数值计算公式，并采用相对成功的初始配置（SIC）方法来验证算法性能。其次，分别采用多分辨率与kd树和邻域搜索相结合的实验，结果表明，当多分辨率与kd树相结合时，速度有所提高，但没有明显提高;当多分辨率与邻域搜索相结合时，SIC范围具有明显的增益效应。实验结果表明，采用多分辨率结合kd树和邻域搜索（特别是结合邻域搜索）可以显著提高 ICP 算法的配准速度。

EM-ICP (2002)

EM-ICP 是S’ebastien Granger 等人提出的一种改进算法，旨在提高算法的鲁棒性和计算时间，同时不降低精度。本文首先给出了场景点与模型点匹配时变化的最大似然估计。基于实际场景中的噪声干扰，给出最大似然估计转换忽略匹配，然后通过贝叶斯估计对上述公式进行优化，但存在无法保证表达式收敛性的问题。

因此，提出了上述两种方法的等效算法 EM算法，以保证算法的收敛性。EM-ICP算法是基于电磁原理，混合高斯噪声，结合退火方案和球面提取技术作为准则，以提高鲁棒性和计算时间的ICP算法。最后，选取两组异质但精确的数据和同质但有噪声的数据进行实验。结果表明，EM-ICP在困难条件下具有很强的鲁棒性。并在精细范围内接近ICP算法。EM-ICP具有比ICP更好的鲁棒性和性能。

Point-to-Plane ICP（2004）

原始 ICP 算法的代价函数中使用的 point-to-point 距离，point-to-plane 则是考虑源顶点到目标顶点所在面的距离，比起直接计算点到点距离，考虑了点云的局部结构，精度更高，不容易陷入局部最优；但要注意 point-to-plane 的优化是一个非线性问题，速度比较慢，一般使用其线性化近似。

G-ICP（2009）

Generalized-ICP（G-ICP）是由Aleksandr V. Segal等人提出的概率框架，它结合了标准ICP算法和point to plane ICP算法。它是一种改进的算法，保持了ICP算法的速度和简单性，提高了准确性。

G-ICP 介于标准和完全概率模型之间，适用于大型点云数据。通过两次扫描可以建立局部平面结构模型，可以看作是 Plane-to-plane ICP。G-ICP算法的基本原理是在标准ICP算法中的最小平方函数上附加一个概率模型，并保持 ICP 的其余步骤不变。

Scale-ICP （2009）

Scale-ICP 是 Shihui Ying 等人提出的一种改进的ICP算法，适用于尺度变化。本文通过引入具有上下界的比例因子，将标准ICP算法转化为7D非线性空间中的二次约束优化问题，并利用奇异值分解（SVD）对标准ICP算法的迭代过程进行优化。讨论如何选择一个好的初始注册以达到全局最小值。

从两个方面进行了实验：一是标准ICP算法与 Scale-ICP 算法的比较。实验结果表明，Scale-ICP 的精度高于 ICP 的精度;其次，为实验选择五个不同的初始值。结果表明，Scale-ICP 对不同尺度数据集具有较好的配准鲁棒性。

GO-ICP (2015)

GO-ICP 是 Jiaolong Yang 等基于分支绑定（BnB）理论提出的一种全局优化算法。该方法使用 $SE(3)$ 的特殊结构给出配准误差函数的上限和下限。结合THE BnB算法，不仅保证了全局最优性，而且加快了配准速度。

首先提出了需要优化和改进的公式，然后引入了强大的全局优化技术，从而将 2D 环境中的 BNB 提高到 3D 水平，提出了解决方案：参数化3D移动区域并有效找到函数的上下界。边界函数是通过引入不确定性半径得出的。最后，提出GO-ICP算法：利用嵌套BNB对数据集进行缩减，避免冗余操作步骤，并给出算法终止条件。将BnB和ICP算法集成，使两种算法收敛到全局最小值互补，提高效率。

在实验部分，利用BNB的收敛条件，利用DT和kd树验证了推导边界的正确性和GO-ICP的最优性。对于全局和局部注册，选择了十个从不同方向扫描的点云数据集，并讨论了点、噪声、收敛阈值和最佳误差的影响。讨论了部分重叠登记，并介绍了适用于GO-ICP算法的另外几种情况。实验结果表明，GO-ICP不需要一个好的初始值，当需要精确的全局最优解或初始化值不可靠时，它非常有效。

Fast Global Registration (2017)

一种基于几何特征的配准算法，能够快速、准确地对点云进行配准。由西班牙巴塞罗那自治大学的 J. A. Bagnell等人于2017年提出。相比于传统的ICP算法和其变体，FGR具有更高的速度和更强的鲁棒性，在实际应用中取得了不错的效果。FGR算法基于点对之间的法向量、距离和相对姿态进行匹配。与ICP算法不同的是，FGR首先将源点云和目标点云分别进行降采样，然后计算它们之间的几何特征。这些特征包括法向量、球面坐标、法向量协方差矩阵、曲率等等。接下来，FGR使用一种基于特征的快速匹配方法，将源点云的每个点与目标点云的一些候选点进行匹配，找到最优的匹配点对。在找到匹配点对之后，FGR使用一个全局优化算法来进一步优化匹配结果。具体来说，FGR使用了一种基于四元数的全局优化方法，它能够最小化点云之间的欧氏距离误差，从而得到更准确的配准结果。此外，FGR还考虑了一些对鲁棒性有帮助的技巧，如一些限制条件和一个迭代过程中的逐步加权策略。

GF-ICP (2017)

GF-ICP 是 He, Ying 等人提出的基于几何特征的改进 ICP 算法，利用两组待注册点云数据的曲率、表面法线和点云密度等几何特征来搜索对应的点，并将几何特征引入ICP算法的误差函数表达式中，从而实现精确的点云注册。

用曲率和表面法线来表示特征参数，并检测模型的几何特征。数据变化密集的区域为特征区域，而面积变化较小的区域为非特征区域。GF-ICP算法的步骤与ICP算法的步骤总体上是相同的。不同的是在寻找最近点时使用了数据的几何特征参数。如果参数满足设定的阈值，则两点被认为是对应点。此外，曲率和法线角这两个影响因素被加入误差函数中进行迭代计算，直到满足阈值条件或达到最大迭代次数，迭代结束。文章在四种不同条件下对ICP、kd-tree ICP和GF-ICP三种算法进行了比较，即对算法的精度和速度、套准的重合度、噪声的抗干扰能力和现实的大尺度数据进行了分析，实验结果表明，GF-ICP算法，迭代次数少，收敛范围大，初始位置不是很理想，或有少量噪声，都能获得良好的套准效果。

N-ICP (2017) Github

NICP是一种用于递归地对齐点云的在线方法。该方法利用三维结构来确定两个云之间的数据关联，同时考虑到每个点和其表面的局部特征：法线和曲率。该方法采用视线标准来寻找两片云之间的对应点进行注册。这与NICP使用的高效算法和数据结构一起，提高了该方法的速度，允许实时计算。NICP 通过采用最小二乘法来解决对齐问题，最小化一个取决于点坐标和相关法线的误差指标。这使得该算法更加稳健和准确，从而计算出更好的变换。

kd-tree ICP (2020)

kd-tree ICP 是 Shi, Xiaojing 等人提出的基于kd-树并结合点云滤波和自适应烟花算法的改进ICP算法，该算法利用点云滤波和自适应烟花算法首先完成点云数据的粗注册，然后利用kd-树改进ICP算法，完成精细注册。

文章首先讨论了点云数据的滤波，通过kd-tree找到相应的点，并计算它们之间的平均距离，与设定的距离条件进行比较，剔除异常值。然后讨论了基于自适应焰火算法的粗注册，介绍了从基本焰火算法到自适应焰火算法的演化过程，并提出了基于改进后的焰火算法的自适应爆炸半径机制。最后，利用烟花自适应算法得到的粗注册结果作为精细注册的初始位置，用改进的 kd-tree ICP 算法进行精细注册。

在实验中，分析了kd-tree ICP算法的点云注册误差和注册稳定性，并与其他算法的计算效率进行了比较。实验结果表明，该算法的粗注册可以获得较好的初始位置，从而大大减少了精细注册的计算时间，在保证精度的同时提高了计算速度，具有较好的稳定性。

目录CONTENT

点云 ICP 配准算法

定义