IMU原理与模型 未完成

IMU 的工作原理

简介

IMU 惯性测量单元(Inertial Measurement Unit) 是测量物体三轴角速度和加速度的设备。一个IMU内在正交的三轴上安装陀螺仪和加速度计，共6个自由度，分类测量角速度和加速度， 称为6轴 IMU；一个 IMU 可在加速度计和陀螺仪的基础上加入磁力计，就形成了9轴IMU

增加了磁力计的 9轴传感器 又被称为 AHRS 航姿参考系统(Attitude and Heading Reference System)。因为航向角有地磁场的参考，所以不会漂移，但地磁场很微弱，经常受到周围带磁场物体的干扰。磁场和重力场越正交，则航姿测量效果越好，也就是说如果磁场和重力场平行，比如地磁南北极，AHRS 就没法使用。

加速度计

加速度计是一种惯性传感器，能够测量物体的加速力。加速力就是当物体在加速过程中作用在物体上的力，就比如地球引力，也就是重力。
目前常用的加速度计使用 MEMS 技术制造的加速度计。由于采用了微机电系统技术，使得其尺寸大大缩小.

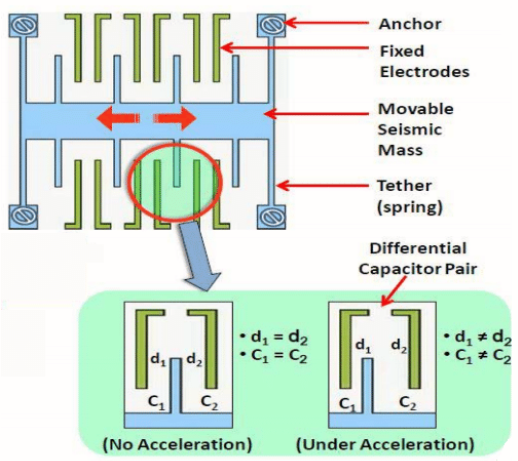
容感式MEMS加速度计内部也存在一个质量块，从单个单元来看，它是标准的平板电容器。加速度的变化带动活动质量块的移动从而改变平板电容两极的间距和正对面积，通过测量电容变化量来计算加速度。

陀螺仪

MEMS陀螺仪主要利用科里奥利力（旋转物体在有径向运动时所受到的切向力）原理，公开的微机械陀螺仪均采用振动物体传感角速度的概念，利用振动来诱导和探测科里奥利力。

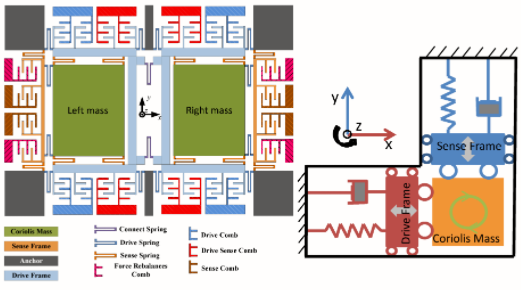
MEMS 陀螺仪的核心是一个微加工机械单元，在设计上按照一个音叉机制共振运动，通过科里奥利力原理把角速率转换成一个特定感测结构的位移。

两个相同的质量块以方向相反的做水平震荡。当外部施加一个角速率，就会出现一个科氏力，力的方向垂直于质量运动方向，如垂直方向箭头所示。产生的科氏力使感测质量发生位移，位移大小与所施加的角速率大小成正比，科氏力引起的电容变化即可计算出角速率大小。

磁力计

磁力计能提供装置在XYZ各轴所承受磁场的数据，以提供磁北极相关的航向角，利用这些信息可侦测地理方位。

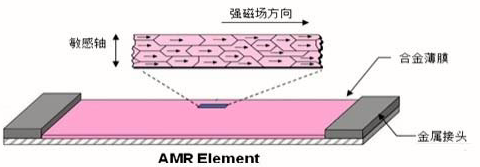
上图为一种采用具有晶体结构的合金材料。它们对外界的磁场很敏感，磁场的强弱变化会导致磁阻传感器电阻值发生变化。

IMU 的误差模型

误差可以分为：确定性误差，随机误差。

• 确定性误差可以事先标定确定，包括： bias , scale 等。
  – Bias：理论上，当没有外部作用时，IMU 传感器的输出应该为0。但是，实际数据存在一个偏置b。
  – Scale：scale 可以看成是实际数值和传感器输出值之间的比值（电信号到模拟信号，单位不同会通过一个 scale 的转化，这个 scale 会存在误差）。
  –非正交误差： 多轴 IMU 传感器制作的时候，由于制作工艺的问题，会使得xyz轴可能不垂直。
• 随机误差通常假设噪声服从高斯分布，确定其方差大小，包括：高斯白噪声， bias随机游走等。

IMU的误差来主要来自于三部分，包括噪声(Bias and Noise)、尺度因子(Scale errors)、轴偏差(Axis misalignments)。加速度计和陀螺仪的测量模型可以用式(1.1)和式(1.2)表达。

$$\begin{aligned} a^{B} & =T^{a} K^{a}\left(a^{S}+b^{a}+\nu^{a}\right) \end{aligned}\tag{1.1}$$

$$\begin{aligned} w^{B} & =T^{g} K^{g}\left(w^{S}+b^{g}+\nu^{g}\right) \end{aligned}\tag{1.2}$$

其中上标 $a$ 表示加速度计，$g$ 表示陀螺仪，$B$ 表示正交的参考坐标系，$S$ 表示非正交的选准坐标系。$T$ 表示轴偏差的变换矩阵，$K$ 表示尺度因子，$a^{S}$,$w^{S}$ 表示真值，$b$,$ν$ 分别表示Bias和白噪声。

IMU噪声模型(Bias and Noise)

对IMU的噪声模型进行重新的定义，去除其误差模型中的轴偏差和尺度因子，可以将IMU的噪声模型写为，

$$\tilde{\omega}(t)=\omega(t)+b(t)+n(t)$$

其中 $n(t)$ 表示高斯白噪声，$b(t)$ 表示随机游走噪声。下面就这两种噪声的具体形式和来源展开说明。

高斯白噪声

服从高斯分布的一种白噪声，其一阶矩为常数，二阶距随时间会发生变化。一般来说这种噪声是由AD转换器引起的一种外部噪声。因为连续的高斯白噪声服从如下条件，

$$E(n(t)) \equiv 0$$

$$E\left(n\left(t_{1}\right) n\left(t_{2}\right)\right)=\sigma_{g}^{2} \delta\left(t_{1}-t_{2}\right)$$

其中 $\delta(t)$ 表示狄拉克函数。$\sigma_{g}$ 位高斯白噪声的方差，值越大，表示噪声程度越大。将其进一步离散化后，得到，

$$n_{d}[k]=\sigma_{g d} \omega[k]$$

其中$\omega[k] \sim N(0,1)$，$\sigma_{g d}=\sigma_{g} \frac{1}{\sqrt{\Delta t}}$。

证明如下，

$$n_{d}[k]=n\left(t_{0}+\Delta t\right) \simeq \frac{1}{\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(\tau) d \tau$$

$$\begin{aligned} E\left(n_{d}[k]^{2}\right) & =E\left(\frac{1}{\Delta t^{2}} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(\tau) n(t) d \tau d t\right) \\ & =\frac{\sigma_{g}^{2}}{\Delta t^{2}} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} \delta(t-\tau) d \tau d t \\ & =\frac{\sigma_{g}^{2}}{\Delta t} \end{aligned}$$

则有 $\sigma_{gd}^{2}=\frac{\sigma_{g}^{2}}{\Delta t}$，即 $\sigma_{g d}=\sigma_{g} \frac{1}{\sqrt{\Delta t}}$。

随机游走噪声(这里指零偏Bias)

随机游走是一个离散模型，可以把它看做是一种布朗运动，或者将其称之为维纳过程。该模型可以看做是高斯白噪声的积分。该噪声参数一般是由传感器的内部构造、温度等变化量综合影响下的结果。

$$b_{g} \dot{(}t)=\sigma_{b g} \omega(t)$$

其中 $\omega(t)$ 是单位的高斯白噪声，在上面提到了。如果把随机游走噪声离散化，可以写作：

$$b_{d}[k]=b_{d}[k-1]+\sigma_{b g d} \omega[k]$$

其中，$\omega[k] \sim(0,1), \quad \sigma_{b g d}=\sigma_{b g} \sqrt{\triangle t}$。

由随机游走的分布可以看出，随机游走都是在上一次的噪声的基础之上叠加了一个高斯噪声，所以下一步永远都是随机的。

IMU尺度因子

其实在这个地方上说IMU的尺度因子不太恰当，应该将其称之为尺度误差。这部分的误差来自于传感器的数字信号向物理量转换的误差，比如说AD向加速度/角速度转换的时候的误差。尺度误差的表达比较简单，

$$\begin{aligned} K^{a} & =\left[\begin{array}{ccc}s_{x}^{a} & 0 & 0 \\0 & s_{x}^{a} & 0 \\0 & 0 & s_{x}^{a} \end{array}\right] \\K^{g} & =\left[\begin{array}{ccc}s_{x}^{g} & 0 & 0 \\0 & s_{x}^{g} & 0 \\0 & 0 & s_{x}^{g}\end{array}\right] \end{aligned}$$

IMU轴向误差

一般情况下，加速度计的坐标系AF和陀螺仪的坐标系GF都不是正交的坐标系，但我们正常使用的时候都是默认测量量是在正交坐标系下的，所以就需要一个变换矩阵将测量量从非正交坐标系 AF\GF 下转到正交坐标系 BF 下，将其称之为机体坐标系。

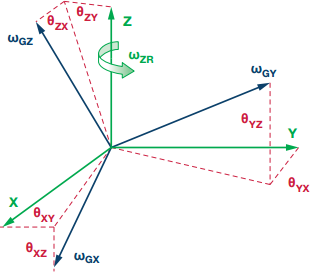
轴向误差一般还伴随着跨轴误差，这两部分一般不加以区分，就放在一起了。所以这部分的误差就是一个变换矩阵，求取实际的旋转坐标系(AF/GF)到参考坐标系(BF)的转换。为了计算变换矩阵，将三个轴偏角分解，将每个轴向的偏差角沿着另外两个轴分解即可得到。

$$s^B=T s^A, \quad T=\left[\begin{array}{ccc}1 & -\theta_{y z} & \theta_{z y} \\ \theta_{x z} & 1 & -\theta_ {z x} \\ \theta_{x y} & \theta_{y x} & 1\end{array}\right]$$

IMU 的标定方法

什么是标定

标定，也称校准，是对单个传感器的优化，使其消除系统误差，改善仪器或系统的精确度。

标定的本质是参数辨识，根据实验数据和建立的模型来确定一组模型的参数值。

目前常用的传感器标定方法有：

• 解析法或最小二乘法
• 滤波法
• 迭代优化法

IMU 的标定

IMU 在标定过程中，加速度计和陀螺仪是分开标定的，一般是先标定加速度计，然后利用准确的加速度计信息再来标定陀螺仪。

目前常用的 IMU 标定方法：

• 基于高精度辅助转台的方法，使用解析法或最小二乘法进行参数辨识
• 另一种是不依赖转台的方法，使用迭代优化的方法进行参数辨识。

整个标定过程的流程如下图所示，

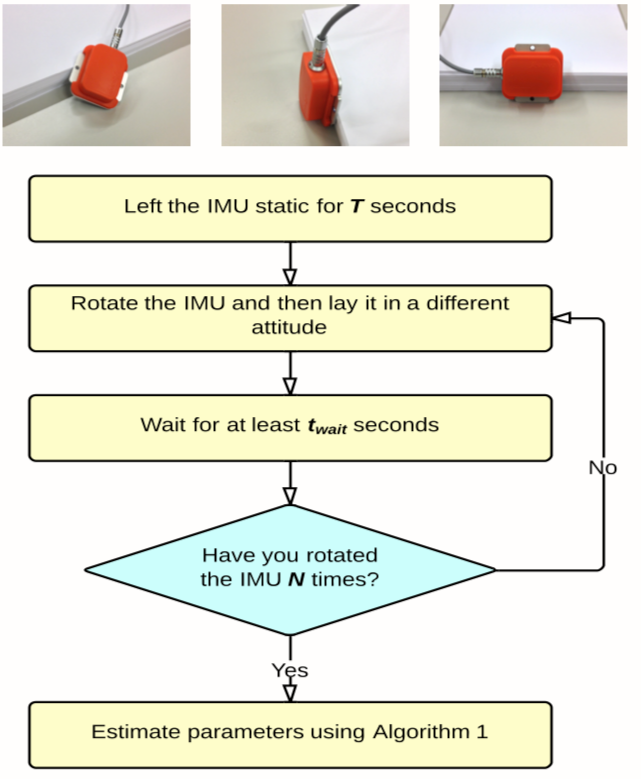
其中，初始化时间 $T$ 一般取50s，旋转后保持静态时间 $t$ 取1∼4s，旋转次数 $N$ 取36∼50 次。一般来说，这个旋转次数越多越好，至少旋转次数要大于要求解的参数的个数，这样才能避免奇异性。

IMU 静态检测

因为在加速度和陀螺仪的校准过程中，常常需要传感器处于静止状态，所以在校准的过程中也就需要判断传感器是否处于静止状态。判断依据也很简单，

$$\varsigma\left(t_w\right)=\sqrt{\left.\left.\left[\operatorname{var}_{t_w}\left(a_x^t\right)\right]^2+\operatorname{var}_{t_w}\left(a_y^t\right)\right]^2+\operatorname{var}_{t_w}\left(a_z^t\right)\right]^2}$$

其中 $\operatorname{var}_{t_w}\left(a^t\right)$ 表示加速度 $a^t$在时间段 $t_w$ 内的方差。
判断的时候，只需将 $\varsigma\left(t_w\right)$ 和 阈值 $\varsigma(T_{init})$比较即可，小于则静态，反之动态。一般取 $T_{init}$ 为50s。

加速度计标定

IMU 的运动模型