基于ROS的相机校准（camera_calibration & image_proc）

相机校准参数的获得（camera_calibration ）

rosrun camera_calibration cameracalibrator.py --size 8x6 --square 0.108 --k 6 image:=/my_camera/image 

** 这里有很多棋盘，分享给大家~ Link

• –size 8x6：棋盘大小为 8x6，仅计算内角
• –square 0.024：棋盘中的一个正方形大小，以米为单位
• –k 6：要使用的径向失真系数的数量（最多6，默认 2)
• image:= 相机发布的图片主题名

运行后订阅 ROS 原始图像主题，并提供一个校准窗口。校准窗口显示来自相机的当前图像，突出显示棋盘格，并记录校准数据，当数据足够时按下校准按钮（否则是灰色的），节点计算相机校准参数。当用户单击COMMIT 时，节点使用服务调用将这些新的校准参数上传到相机驱动程序。
输出的相机校准参数如下：

**** Calibrating ****
mono pinhole calibration...
D = [14.565826177152536, 10.477393040343149, 1.6097304996818903e-05, -0.0038758664891502346, -21.615524616819467, 14.51314595032321, 9.0117176329534, -20.246159366771483]
K = [622.7139809471598, 0.0, 632.8545193623008, 0.0, 625.5215201440889, 369.59461579516187, 0.0, 0.0, 1.0]
R = [1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0]
P = [666.8020629882812, 0.0, 618.1466074989657, 0.0, 0.0, 662.8768310546875, 369.8623347548855, 0.0, 0.0, 0.0, 1.0, 0.0]
None
# oST version 5.0 parameters


[image]

width
1280

height
720

[narrow_stereo]

camera matrix
622.713981 0.000000 632.854519
0.000000 625.521520 369.594616
0.000000 0.000000 1.000000

distortion
14.565826 10.477393 0.000016 -0.003876 -21.615525 14.513146 9.011718 -20.246159

rectification
1.000000 0.000000 0.000000
0.000000 1.000000 0.000000
0.000000 0.000000 1.000000

projection
666.802063 0.000000 618.146607 0.000000
0.000000 662.876831 369.862335 0.000000
0.000000 0.000000 1.000000 0.000000

*参考网站链接：link

参数分析

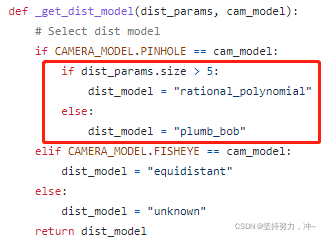
失真模型

对于针孔型相机，失真模型分为为plumb_bob和rational_polynomial，具体取决于使用的径向畸变参数K的数量，当K为6时是rational_polynomial模型，其他则为plumb_bob。

D、K、R、P参数

在完成校正后我们得到D、K、R、P参数矩阵。
D参数：相机的失真系数，属于相机的内在参数，它最少可以是4个参数，最多为8个。其中，k1, k2, k3, k4, k5, 和 k6是径向畸变系数。 p1是切 p2向畸变系数。具体推导过程：link

$$\left(k_{1}, k_{2}, p_{1}, p_{2}\left[, k_{3}\left[, k_{4}, k_{5}, k_{6}\right]\right]\right)$$

K参数：为相机矩阵，cx, cy是通常位于图像中心的主点，fx, fy是以像素为单位表示的焦距。

$$\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]$$

R参数：通常为单位矩阵，如果需要旋转也可以加。
P参数：冗余信息，在普通单目中可以直接由K形成

利用校准参数校正图像（image_proc）

    <!-- 生成一个 image_proc/rectify nodelet 来校正 RGB 图像 -->
    <node pkg="nodelet" type="nodelet" name="rectify_rgb_1"
          args="load image_proc/rectify manager_1 --no-bond"
          respawn="true">
      <!-- image_mono：未矫正的的图像  image_rect经过校正后的图像  -->
      <remap from="image_mono"  to="rgb_to_depth/image_raw" />
      <param name="interpolation"  value="0" />
      <param name="queue_size"  value="2" />
      <remap from="camera_info"  to="rgb_to_depth/camera_info" />
      <remap from="image_rect"  to="rgb_to_depth/image_rect" />
    </node>

通过获取未校正的图像流及其相关的校准参数，并生成校正后的图像。
*参考网站链接：link

校正过程，重点！！！

• 我们先看上面一行的原图转化过程：首先对于空间中的一点X，通过Rt矩阵与投影操作（除以Z）将点投影到标准化的未失真图像上，而每一个相机实际上都存在镜片畸变，假设其畸变矩阵为D，并将点移动到其失真位置，目前仍然在归一化图像中。最后，通过将相机矩阵应用于每个图像点，将归一化图像转换为像素坐标图像，这也就是我们所得到的相机原图。
• 校正过程则是为了去掉畸变影响，首先对原图KD的逆变化得到标准化的未失真图像，旋转R是单位矩阵，因为我们不想旋转归一化的未失真图像。然后K’转换到未畸变的输出图像中的像素坐标，由于不需要在图像平面内平移或从原始图像缩放，所以直接使用K = K’（我们也可以用camera_calibration进行单目校准获得的优化过的K来映射更好）。

*参考网站链接：link