环境感知方式
机器人获取环境信息的方式是多种多样的,常用的几个我们将它分为以下几类:
- 激光雷达,包括2D和3D雷达。
- 纯视觉,包括单目相机和双目相机
- 视觉加深度感知,包括红外结构光相机和TOF相机等。
以上的方法都有各自的优缺点,在复杂环境下通常我们需要其中的组合融合方式来提高系统的鲁棒性。
2D激光雷达数学模型
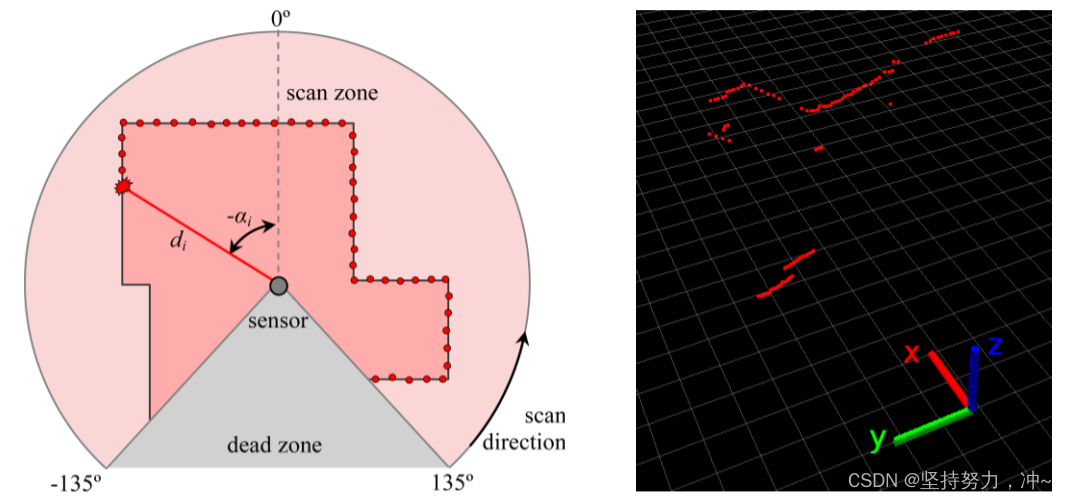
二维激光雷达是由一束在平面上旋转的激光束和一个测量反射光的飞行时间的接收器组成的。对于每个激光方向,传感器记录一个距离,计算为飞行时间的一半乘以光速。结果是距离 di 的大小为n的向量,每个向量都与方位方位 αi 相关联:[d1,d2,d3……dn]。
上图中,一个2D激光雷达对每1度进行距离测量,从−135°到+135°进行扫描(由于自身遮挡问题,使得扫描时需要设置死区),则由270个距离d和角度值α构成完整的激光扫描。而d和α值能够直观的在极坐标中表示,而在笛卡尔坐标系中则需要转换:πiS=[xiS,yiS]⊤。
[αidi]=polar2(πS)≜[arctan(yS,xS)(yS)2+(xS)2]
其中我们定义:
- ∗S在传感器框架中
通过传感器位姿(p,θ)在全局坐标系中表示,得到完整的观测模型:
[αidi]=polar2(R{θ}(π−p))
在已知传感器位姿(p, θ)的情况下,将接收回波[αi , di]转换为全局二维笛卡尔坐标系,得到反观测模型:
πi=p+diR{θ}[cosαisinαi]
通常我们需要注意车辆运动速度,因为在扫描过程中,车辆的位置和方向可能不是恒定的(典型的2D扫描周期大约为100ms)。为此,只要车辆姿态时刻对应于感知到回波点的时刻,上述公式对于每个回波点都是有效的。所以我们引入 ti 作为与回声 i 相关的时间:
πi=p(ti)+diR{θ(ti)}[cosαisinαi]
在[p(t),θ(t)]的姿势传感器在时间 t 。时间 ti 可以很容易地恢复扫描时间戳 TS[s] ,扫描速度 ω(rad/s) ,和回声密度 δ(echoes/rad) (公式可能承认根据扫描的方式是带时间戳的细微变化;这里,我们认为 TS 对应于回声 i0),
ti=TS+δ⋅ωi−i0
3D激光雷达数学模型
3D激光雷达有两种实现方式:一种是将2D的安装在一个可控倾斜的平台上以探测不同角度的平面,另一种是使用一组旋转光束,每一束都有不同的倾角或高度。
2D雷达式
在这种情况下,通过控制雷达的倾斜摆动来实现3D建模,其感知模型与二维激光雷达的感知模型是相同,只是考虑了三维的框架变换,而不是原本的平面二维。
为了简化推导,现在只考虑激光扫描平面切片中的π点,具有零Z分量的局部点πS,并将其XY分量转换到极坐标下形成扫描读数,即绕XY面上通过原点的轴进行倾斜摇摆:
[αidi]=polar2(R{q(ti)}(πi−p(ti))∣XY)
对于反演观测模型,我们只需要将每个二维扫描转换为其三维笛卡尔方向,就可以在三维空间中构建完整的三维扫描模型:
πi=p(ti)+diR{q(ti)}⎣⎢⎡cosαisinαi0⎦⎥⎤
在这种方式下由于我们还要考虑车辆的相对运动,而且其倾斜运动通常非常缓慢,以便进行完整的倾斜循环扫描。通常,完整的一次扫描需要一秒或更多的时间来完成。这一事实严重限制了车辆的最大速度,因为快速扫描会降低扫描结果模型的密度。
旋转光束式
这种方案下,一组M个旋转光束在不同仰角ϵj,j∈1···M,平行绕垂直轴转动。因此,传感器输出是一个范围矩阵:
⎣⎢⎢⎢⎢⎡d11d21⋮dM1d12d22dM2⋯⋯⋯d1Nd2NdMN⎦⎥⎥⎥⎥⎤
其中每一行对应高度ϵj,每一列对应方位αi。该几何模型与倾斜的2D扫描仪的不同之处在于,由于不同的仰角,大多数光束不像在2D情况下那样探测一个平面,而是一个圆锥(除了最中间的扫描通道)。
我们使用3D极坐标:
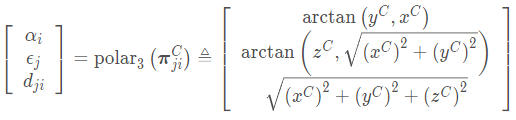
我们也可以变换到移动机器人上,得到极坐标下的观测模型:
⎣⎢⎡αiϵjdji⎦⎥⎤=polar3(R{q(ti)}(πji−p(ti)))
而在正常的笛卡尔坐标系中:
πji=p(ti)+djiR{q(ti)}⎣⎢⎡cosαicosϵjsinαicosϵjsinϵj⎦⎥⎤
所有点的集合πji形成了一个三维点云。在这里,完整的3D点云可以在100ms量级的单次扫描中完成,因此在同等的扫描密度下允许更高的车辆速度。最后请注意,只有对于一个零标高(最中间的)的光束ϵj= 0,扫描是平面的,并且公式与倾斜的2D扫描仪的公式相匹,因为其余的是锥面。
单目相机数学模型
先鸽一鸽,有思维导图,要的关注私信一下
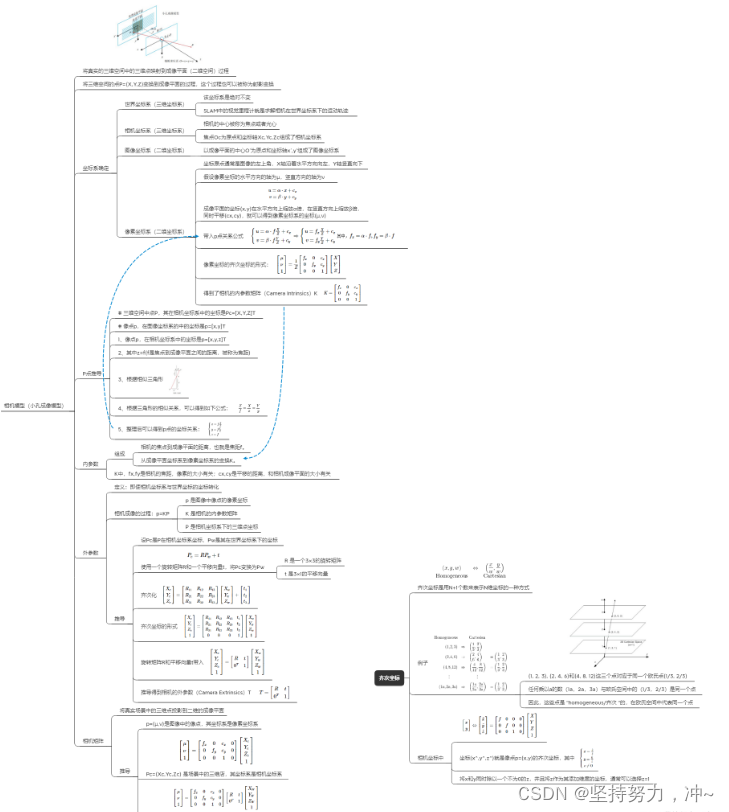
双目相机数学模型
RGBD相机数学模型

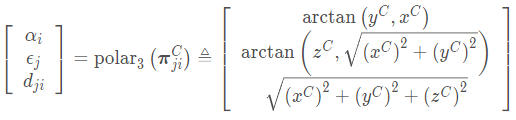





评论区