#4 SLAM_Transformation Matrices(变换矩阵)

基础功能

• 来表示全局坐标系中相对坐标系的方向和位置
• 将一个坐标系的点或向量，映射到另一个坐标系
• 对点或向量在同一坐标系中进行缩放、旋转和平移之类的变换

变换矩阵对参考系的操作(重点)

首先来看一个点在参考系旋转变换中的过程。

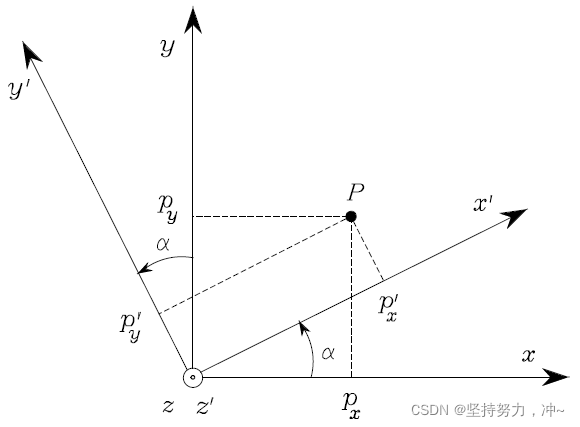
描述：上图中存在一个参考坐标系 $xyz$ ，并存在一点 $P$，通过旋转 $\alpha$ 度到 ${x}' {y}' {z}'$，则在 ${x}' {y}' {z}'$ 下为 ${P}'$。(注意，目前只是旋转了参考坐标系，点并没有动！！在SLAM中则是以第一帧为世界坐标系，之后的移动帧向其变换，所有的点都在世界坐标系下)。则有等式：

$$P=\boldsymbol{R}(\alpha) P^{\prime}$$

请注意！！！：原坐标的点在左边，而 $P^{\prime}$ 需要旋转后才与 $P$ 的坐标值相同。因为点没动，只是相对的坐标值变了。

现在当我们继续对坐标系进行旋转操作，那就分成了两种情况：

• 以自身 ${x}' {y}' {z}'$ 为基准进行变换
• 以参考坐标系 $xyz$ 作为基准，继续对 ${x}' {y}' {z}'$ 进行变换

2D平面中

相对自身参考坐标系连续变换

为了方便列式子，我们将世界参考系设为0号，对后续的连续旋转变换设为，1，2，3……$N$，则：

• 参考坐标系1相对于坐标系0的旋转矩阵，记为 $\boldsymbol{R}_{1}^{0}$ ；
• 参考坐标系2相对于坐标系1的旋转矩阵，记为 $\boldsymbol{R}_{2}^{1}$ ；
• 参考坐标系2相对于坐标系0的旋转矩阵，记为 $\boldsymbol{R}_{2}^{0}$ ；
• 同样假设世界坐标系中有一点$P^{0}$，而在其他的顺推为：$P^{1}$，$P^{2}$……
• 注意：这里的$\boldsymbol{R}$的每次旋转是相对于自身，例如 $\boldsymbol{R}_{2}^{1}$，是绕坐标系1的轴进行R变换到坐标系2，也就是相对于上一个坐标系。
  在这样的规则下可以得到以下式子：

$$\begin{array}{l} P^{1}=\boldsymbol{R}_{2}^{1}P^{2} \\P^{0}=\boldsymbol{R}_{1}^{0} P^{1} \\P^{0}=\boldsymbol{R}_{1}^{0} \boldsymbol{R}_{2}^{1}P^{2} \\P^{0}=\boldsymbol{R}_{2}^{0} P^{2} \end{array}$$

简化为：

$$\boldsymbol{R}_{2}^{0}=\boldsymbol{R} _{1}^{0} \boldsymbol{R}_{2}^{1}$$

由此我们可以观察到：相对自身参考坐标系连续变换，旋转变换矩阵按序右乘。

相对世界参考坐标系连续变换

同样我们将世界参考系设为0号，对后续的连续旋转变换设为，1，2，3……$N$，则：

• 参考坐标系1相对于坐标系0的旋转，相对于世界坐标系的旋转矩阵，记为 $\boldsymbol{\bar{R}}_{1}^{0}$ ；
• 参考坐标系2相对于坐标系1的旋转，相对于世界坐标系的旋转矩阵，记为 $\boldsymbol{\bar{R}}_{2}^{1}$ ；
• 参考坐标系2相对于坐标系0的旋转，相对于世界坐标系的旋转矩阵，记为 $\boldsymbol{\bar{R}}_{2}^{0}$ ；
• 同样假设世界坐标系中有一点$P^{0}$，而在其他的顺推为：$P^{1}$，$P^{2}$……
• 注意：这里的$\boldsymbol{\bar{R}}$的每次旋转都是相对于世界固定参考系，例如 $\boldsymbol{\bar{R}}_{2}^{1}$，是绕世界坐标系0的轴进行R变换从坐标系1到坐标系2。
  在这样的规则下可以得到以下式子：

$$\begin{array}{l} P^{0}=\boldsymbol{\bar{R}}_{1}^{0} P^{1} \\P^{0}=\boldsymbol{\bar{R}}_{2}^{1}\boldsymbol{\bar{R}}_{1}^{0}P^{2} \end{array}$$

这里我们其实可以看作将$\boldsymbol{\bar{R}}_{2}^{1}\boldsymbol{\bar{R}}_{1}^{0}$看作为$\boldsymbol{\bar{R}}_{2}^{0}$的拆开表达。

3D平面中

相对自身参考坐标系连续变换

描述：从世界参考系 $A$ 开始。对参考系 $B$ 首先绕 $\hat{\mathrm{Z}}_{B}$ 旋转 $\alpha$ ，然后绕$\hat{\mathrm{Y}}_{B}$ 旋转 $\beta$ ，最后绕$\hat{\mathrm{X}}_{B}$旋转 $\gamma$。

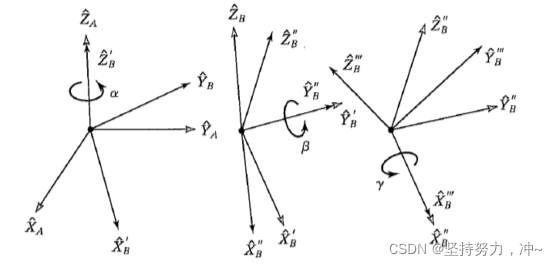
旋转发生在不同的坐标系中:$\{\mathrm{A}\} \rightarrow\left\{\mathrm{B}^{\prime}\right\} \rightarrow\left\{\mathrm{B}^{\prime \prime}\right\} \rightarrow\{\mathrm{B}\}$

依据2D的推导扩展到3D，同样可得到：

$${ }_{B}^{A} R={ }_{B^{\prime}}^{A} R_{B^{\prime \prime}}^{B^{\prime}} R_{B}^{B^{\prime \prime}} R$$

$$\begin{aligned} { }_{B}^{A} R_{Z^{\prime} Y^{\prime} X^{\prime}} &=R_{Z}(\alpha) R_{Y}(\beta) R_{X}(\gamma) =\left[\begin{array}{ccc}c \alpha & -s \alpha & 0 \\ s \alpha & c \alpha & 0 \\0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}c \beta & 0 & s \beta \\0 & 1 & 0 \\ -s \beta & 0 & c \beta\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & c \gamma & -s \gamma \\0 & s \gamma & c \gamma\end{array}\right]\end{aligned}$$

$${ }_{B}^{A} R_{Z^{\prime} Y^{\prime} X^{\prime}}(\alpha, \beta, \gamma)=\left[\begin{array}{ccc} c \alpha c \beta & c \alpha s \beta s \gamma-s \alpha c \gamma & c \alpha s \beta c \gamma+s \alpha s \gamma \\ s \alpha c \beta & s \alpha s \beta s \gamma+c \alpha c \gamma & s \alpha s \beta c \gamma-c \alpha s \gamma \\ -s \beta & c \beta s \gamma & c \beta c \gamma \end{array}\right]$$

相对世界参考坐标系连续变换

描述：从世界参考系 $A$ 开始。对参考系 $B$ 首先绕 $\hat{\mathrm{X}}_{A}$ 旋转 $\gamma$ ，然后绕$\hat{\mathrm{Y}}_{A}$ 旋转 $\beta$ ，最后绕$\hat{\mathrm{Z}}_{A}$旋转 $\alpha$。

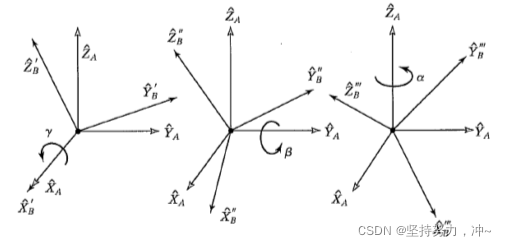
旋转发生在同一坐标系 $A$ ，可以认为是一个连续的旋转操作。
依据2D的推导扩展到3D，同样可得到：

$$\begin{aligned} { }_{B}^{A} R_{X Y Z}(\gamma, \beta, \alpha) &=R_{Z}(\alpha) R_{Y}(\beta) R_{X}(\gamma) =\left[\begin{array}{ccc} c \alpha & -s \alpha & 0 \\s \alpha & c \alpha & 0 \\0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}c \beta & 0 & s \beta \\0 & 1 & 0 \\-s \beta & 0 & c \beta\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 0 \\0 & c \gamma & -s \gamma \\0 & s \gamma & c \gamma\end{array}\right]\end{aligned}$$

$${ }_{B}^{A} R_{X Y Z}(\gamma, \beta, \alpha)=\left[\begin{array}{ccc} c \alpha c \beta & c \alpha s \beta s \gamma-s \alpha c \gamma & c \alpha s \beta c \gamma+s \alpha s \gamma \\ s \alpha c \beta & s \alpha s \beta s \gamma+c \alpha c \gamma & s \alpha s \beta c \gamma-c \alpha s \gamma \\ -s \beta & c \beta s \gamma & c \beta c \gamma \end{array}\right]$$

变换矩阵对点或向量的操作

平移、旋转、缩放和剪切的任何组合都可以组合在一个 4 x 4 仿射变换矩阵中：

$$\mathbf{M}=\left(\begin{array}{cccc} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & 0 & 1 \end{array}\right)$$

当对点或向量操作时，这样一个 4 x 4 矩阵 M 对应于一个仿射变换 T () ，它将点或向量 x 变换为点或向量 y。如上所示矩阵的左上角 3 × 3 子矩阵表示旋转变换，其中也可以包括缩放和剪切。矩阵的最后一列代表一个平移。点 x 到点 x ’ 的变换 T () 通过矩阵-向量乘法得到 :

$$\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\1\end{array}\right)=\mathbf{M}\left(\begin{array}{l}x \\y \\z \\1 \end{array}\right)$$

变换矩阵 M 使用齐次坐标，可以区分点和向量。向量具有方向和大小，而点是相对于原点的坐标位置。点和向量都表示为齐次坐标中的数学列向量，不同之处在于点在第四行位置具有 1 而向量在该位置具有 0 ，这是为了消除平移操作（第 4 列）对向量的影响。

即变换矩阵 M ，矩阵的最后一行始终是 (0 0 0 1)，在上面的 3×4 矩阵中留下 12 个参数，用于平移、旋转、缩放和剪切的组合（在第 4 行可用于实现透视图变换）。

平移矩阵

平移矩阵仅沿三个轴中的一个或多个轴移动对象：

$$\mathbf{M}=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right)$$

将平移矩阵应用于点 v 揭示了 Mv 只是将平移向量 $t_{x}$、$t_{y}$ 和 $t_{z}$ 与 v ( $v_{x}$ , $v_{y}$ , $v_{z}$ ) 的分量相加，从而产生平移（移位）：

$$\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right)\left(\begin{array}{c} v_{x} \\v_{y} \\v_{z} \\1 \end{array}\right)=\left(\begin{array}{c} v_{x}+t_{x} \\v_{y}+t_{y} \\v_{z}+t_{z} \\1 \end{array}\right)$$

缩放矩阵

缩放变换通过在矩阵中指定的三个标量值沿三个轴扩展或收缩所有点来更改对象的大小。缩放矩阵具有以下形式：

$$\mathbf{M}=\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

$s_{x}$、$s_{y}$ 和 $s_{z}$ 值分别表示 X、Y 和 Z 维度中的比例因子。将缩放矩阵应用于点 v 会产生一个输出向量，其中每个分量乘以相应的缩放值：

$$\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\left(\begin{array}{c} v_{x} \\ v_{y} \\ v_{z} \\ 1 \end{array}\right)=\left(\begin{array}{c} s_{x} v_{x} \\ s_{y} v_{y} \\ s_{z} v_{z} \\ 1 \end{array}\right)$$

旋转矩阵

旋转矩阵围绕三个坐标轴之一或任意向量旋转对象。旋转矩阵比缩放和平移矩阵更复杂，因为需要整个 3x3 左上角矩阵来表达复杂的旋转。通常使用一系列简单的旋转来指定任意旋转，每此旋转沿着指定顺序（一般默认为xyz）的三个基本轴逐一进行。旋转都是绕给给定轴旋转一个角度，以下三个矩阵 $R_{X}$、$R_{y}$ 和 $R_{z}$ 表示将点围绕坐标原点旋转角度 $θ$ 的变换（以弧度为单位）：

$$\begin{array}{l} \mathbf{R}_{X}(\theta)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos (\theta) & \sin (\theta) & 0 \\ 0 & -\sin (\theta) & \cos (\theta) & 0 \\ 0 & 0 & 0 & 1\end{array}\right) \\ \mathbf{R}_{Y}(\theta)=\left(\begin{array}{cccc} \cos (\theta) & 0 & -\sin (\theta) & 0 \\0 & 1 & 0 & 0 \\ \sin (\theta) & 0 & \cos (\theta) & 0 \\0 & 0 & 0 & 1\end{array}\right) \\ \mathbf{R}_{Z}(\theta)=\left(\begin{array}{cccc} \cos (\theta) & -\sin (\theta) & 0 & 0 \\ \sin (\theta) & \cos (\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{array}\right) \end{array}$$

而且必须进一步定义正角度是执行顺时针 (CW) 还是逆时针 (CCW) 绕轴相对于轴方向的旋转，一般我们定义为是右手坐标系或左手坐标系。

表达空间旋转的还有以下两个常用形式：

欧拉角 (简介)

欧拉角是一组表示空间方向的三个角度。每个角度代表围绕三个正交轴（例如，x、y 和 z 轴）之一的旋转，章动角θ、旋进角（即进动角）ψ和自转角Φ组成。旋转的顺序很重要，因为矩阵乘法是不可交换的。而将方向表示为一组三个角度是直观的，但欧拉角也伴随着一个严重的问题，称为万向节锁定。
因此，欧拉角很难做积分累计运算，或添加其他的限制条件。更好的方法是在给定角度和任意旋转轴的情况下构造一个唯一的变换矩阵。一种优雅的替代方法是使用四元数。

四元数 (简介)

提供了另一种描述旋转的方式。四元数是一个类似于复数的四维量。虽然复数在实部旁边有一个虚部 i ，但四元数的向量分量具有三个虚部 i、j和k。就像旋转矩阵需要一个角度和一个轴来旋转一样，四元数使用角度作为实部，轴在向量（虚部）部分，产生一个表示围绕任何旋转的四元数轴。一系列旋转可以由一系列四元数相乘来表示，产生一个对组合旋转进行编码的单个结果四元数。虽然这也可以通过一系列表示围绕笛卡尔轴的旋转矩阵相乘来实现，但矩阵方法可能会遇到万向节锁定问题。因此，四元数是一种有吸引力的表示旋转的替代方法，因为它们不受万向节锁定的影响。

剪切矩阵

剪切操作“倾斜”物体；它们是通过上部 3 x 3 子矩阵中的非零非对角元素来实现的。例如，表示沿 x 轴的剪切的变换矩阵具有以下形式：

$$\mathbf{S}_{X}(\theta)=\left(\begin{array}{cccc} 1 & \cot (\theta) & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

这个操作很少进行使用。

变换组合

将一个点乘以一系列矩阵可以应用一系列变换。然而，没有必要在每次矩阵向量乘法之后保存中间点。相反，可能通常优选首先将所有矩阵相乘以产生表示整体变换的单个矩阵。然后可以使用该矩阵将点直接从源坐标空间转换到目标坐标空间。转换矩阵的形成过程通常称为串联或矩阵组合。

矩阵的顺序很重要。例如，如果第一个变换将对象绕 Y 轴旋转 45°，而第二个变换将其沿 X 轴平移 10 个单位，则结果与对象先沿 X 轴平移 10 个单位，然后再平移绕 Y 轴旋转 45°是相同的。对于点和向量的列矩阵，以从左到右的形式写，实际上是从右到左应用的。因此，输入向量出现在右侧，而转换序列以相反的顺序（从右到左）运行。因此首先旋转（矩阵R）然后平移（矩阵T）顶点v，可以写成 $u = TRv$，也就是说为左乘操作。

而重要的一点是矩阵乘法一般不是可交换的：矩阵乘积AB通常不等于BA。这意味着如果应用一系列平移、旋转和缩放，则基本变换矩阵出现的顺序对于确定整体变换至关重要。